|
정의상 가정 |
|
|
내용상 가정 |
정상전류를 가정한다.(늘거나 줄지 않고 진로도 바뀌지 않으며 영원히 계속되는 전하의 흐름-> |
|
공식 |
|
|
단위 |
T (SI)자기장을 표현할 때 지름이 1m인 원형 도선에서 1A의 전류를 흘렀을 때 도선 중간에서 나오는 자기장을 1 A/m로 정의 (CGS)1g의 magnetic pole이 1cm/s2의 가속도의 힘을 받을 때를 1 emu |
|
응용 |
magnetic material_AFM(antiferromagnetic), FM(ferromagnetic), paramagnetic, diamagnetic |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
자기장이 다른 어떤 새로운 물리현상이라 생각 할 수 도 있겠지만,
자기장은 단순히 전하가 움직일 때(전류로 존재할 때) 전하의 관성력 입니다.
다시말해 자기는 전하 쿨롱의 법칙(Coulomb's law)의 다른 표현입니다.
정상 전류가 흐르는 다음 도선을 보겠습니다.
보통 전류는 전자의 움직임으로 생기므로 전자만 움직인다고 보았습니다.(물론 양성자도 움직입니다!! 고려해도 양의 차이지 이론적으로 크게 문제가 될게 없어서 전자만 고려하였습니다.)
이런 도선 옆에 정지해있는 전자 하나를 놔두었습니다.
무슨일이 발생할 것 같지만, 아무일도 없습니다.
왜냐하면 정상전류(늘거나 줄지 않고 진로도 바뀌지 않으며 영원히 계속되는 전하의 흐름->)의 경우 도선내에 에너지가 가장 낮은 중성상태를 위한 시간이 지난 후로 도선 자체가 중성입니다.
따라서 옆에 놓은 전자는 아무런 전기적인 힘을 받지 않습니다.
(전하의 쿨롱의 법칙(Coulomb's law)에서 q2가 0입니다!)
이번엔 저 도선 밖에 도선에서 전자가 움직이는 방향과 같은 방향으로 움직이는 전자를 놓아보겠습니다.
도선에서도 도선밖에서 전자가 움직이므로 한번 전자를 멈춰보겠습니다.
즉 움직이는 전자를 상대적인 관성계로 보겠습니다.
상대론을 적용시키면 전자는 다 정지해보이고 양성자만 반대방향으로 움직이는 것 처럼 보입니다.
이때 전자가 정지하며 양성자는 움직이는 것처럼 보입니다.
이때 상대론에 의해 관찰자에 상대적으로 움직이는 물체는 고유길이, 즉 길이가 수축해보입니다. 길이가 수축한다는 함유하는 넓이가 줄어들게 되고 따라서 밀도가 높아지는 것처럼 보입니다!!
즉 도선에 있는 전자의 밀도가 감소하고 양성자의 밀도가 증가하므로(같은 +1q의 전하라도 좁은공간에서 존재하므로) 양성자가 옆에 있는 전자 보다 상대적으로 극성이 커지고 밖에 놔둔 움직이는 전자 입장에서는 도선이 (+)극성으로 보입니다. 따라서 전하의 쿨롱의 법칙(Coulomb's law)에 의해 인력의 힘을 받습니다.
그럼 밖에 있는 전자가 반대방향으로 진행하면 어떻게 될까요??
위랑 똑같이 상대론을 적용하면 도선안의 전자가 빨라서 수축하여 밀도가 높아지고 이번엔 상대적으로 양성자보다 전자의 극성이 높아지게 됩니다!
따라서 밖의 전자가 볼때 도선은 (-)극을 띄게 되고 전가는 인력을 받게 됩니다.
맨날 이렇게 모든 전자에 대해 상대론 적으로 분석하고, 전자의 밀도가 어느정도 늘거나 줄은것을 계산할 수 없으므로 이제 가상의 힘(system)과 그 힘의 체계를 만들어 보겠습니다.
먼저 이 system의 이름은 자기(magnetic) 라고 부르겠습니다.
이 system의 방향은 어떻게 정의할까요??
먼저 움직이는 전자에 대한 것이므로 전자가 움직이는 방향은 반드시 자기의 방향에 포함되어야 합니다.
또한 힘에 대한 것이기 때문에 힘의 방향도 포함시켜야 합니다!
먼저 전자가 움직이는 방향은 고정시켜두고 여러개의 전자를 도선 주변에 놓아보겠습니다.

받는힘이 도선을 주변으로 원을 그리며 퍼지는 방향으로 생기는 것을 알 수 있습니다.
또한 진행 방향과 받는힘이 수직한 관계에 있어 위 그림의 동그란 점선에 어떤 물리량만 붙인다면 진행방향과 받는힘을 연결하는 간단한 수식을 완성할 수 있어 보입니다.
이 물리량의 기호를 동그란 점선을 따라 벡터 B라 한다면
가 되고(v는 진행방향을 속도로 표현했습니다.)
이는 밖의 전자의 전하량이 커질 수록 커지므로
라는 아주 간단한 수식으로 자기장을 정의할 수 있습니다.
자기장을 정의 한것이 전류 주변에 한바퀴 도는 field로 정의했으니 너무도 당연하게 한바퀴로 모두 더한다면 총 알짜힘은 0이 되게됩니다.(장과 힘을 혼용해서 쓰는 이유는 넓은 의미로 장 = 힘이기 때문입니다.)
다시말해 자기장은 다시 돌아와야하여 자기의 극(자극)은 고립되지 않는 총 알짜힘이 0인 특징을 갖는 장입니다.
힘에는 F=ma, 전기력에는 쿨룽의 법칙처럼, 자기력에서도 위의 원리에서 기본적인 법칙을 유도했는데, 이것이 비오-샤바르법칙(Biot Savart Law)입니다.
오직 실험의 결과로만 도출되는 식입니다만, 언듯보면 실험값으로 보이지만, 전류로 전기장을 정의하는 것으로 전류를 흘려주면 자기자이 생기는 현상으로 부터 도출해 낸것입니다. 여기서 µ는 자유공간의 투자율(암페어와 쿨룽을 정의하는데 쓰인다.)이고, 4πx10^(-7)입니다.
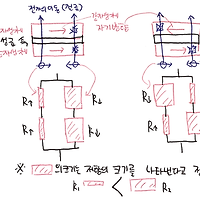
전류에 관련된 모든 자기력 식은(동그란 전류, 원통형 도선 등등)
모두 비오-샤바르 법칙을 적분해서 유도 한 것입니다.
간단하게 예를 들면 다음 그림과 같습니다.
간단한 적분으로 고등과정에서 배우고 있는 모든 식을 유도해 내고
실제로 전자기학의 자기에 관한 문제의 경우 비오-사바르법치과 앙페르법칙만 있으면 모든문제를 간단히 해결 가능합니다!!
왜냐하면 자기에 관한게 이게 끝이기 때문이니까요!!
참고로 이렇게 설명하는 자기장을 SI 단위계에서 자기장이라 합니다.
여기서 의문이 드는게 하나 있습니다.
자기장이 전류에 의해 정의된 개념이라면 익히 알고 있는 "자석"이란 무엇일까요?
물질은 원자로 이루어져 있습니다.
이 원자는 양성자와 전자로 이루어져있는데, 이 원자가 가지고 있는 전자는 자전 운동과 궤도 운동을 하게 됩니다.
즉 전류를 만들어내게 되는 것입니다. 각각의 원자의 전자들이 동일한 방향의 자전, 궤도 운동을 하게 된다면, 자기장이 생겨 한 물질이 외부의 전류에 영향을 미치는, 즉 자기장을 가지게 되는 것입니다.
이때 위 그림에서 유도한 자기 쌍극자 모멘트(Bohr Magnetron)로, 자전운동이 궤도운동보다 휠씬 지배적으로 자기장을 만들어 내 spin에 관한 운동만 물질의 자기장이라 간주할 수 있습니다. (원자와 전자의 상대적 질량비를 생각하시면 왜 지배적인지 알 수 있습니다.)
이때 spin은 위 그림에서 Fe(철) 원자를 표현한 바 파울리 베타원리와 Hund의 법칙에 의해 물질마다 전자쌍을 갖추거나(paired) 갖추지 못한 것(unpaired)이 있는데, 갖추지 못한 것이 더 많을 수록 물질 자체에서 나오는 자기장이 강해집니다.
unpaired가 많아진다고 다 같은 방향의 spin을 같느냐 의심을 가질 수 있겠으나, 정전 에너지가 최소가 되도록 스핀은 배열되는데, 스핀이 평행일 때 에너지가 작아 평행하게 배열되어 커질수있습니다.
물질내 두 전자의 스핀이 반대라 자기장이 상쇄되어 대부분의 물질은 그 자체로 자기장을 띄지 못합니다. 그러나 Fe, Co, Ni 과 같은 물질은 자기장이 완전히 상쇄되지 못합니다. 물론 이러한 물질들도 같은 방향의 스핀을 가진 전자가 모인 구역이 random하게 배열되어 서로 상쇄되어 자기장을 띄지 못할 수도 있습니다.
사실 spin in quantum mechanics에 관한 포스팅을 보신다면, 전자가 자전 운동을 한다는 것은 그저 가설일 뿐입니다.
스핀이 발견된건 전자가 외부 자기장에의해 2방향으로 휜다는 것 때문에 발견되었고 아직도 이 스핀의 정확한 물리적 실체에 대해선 아는바가 없습니다.
잠시 spin을 유도한 방정식 속에서 유도한다면(quark theory)
공전 전자의 경우
이고 자전전자의 경우
이때 proton의 경우 질량이 전자보다 커서 momentum이 작습니다.
이 스핀의 물리적 실체가 전하가 아닌 정말로 자기장이 그 원천이라면, 지금까지 논의 된 바와 반대로, 자기장이 본래 근본 원리고, 전하는 자기장에서 파생되어 그저 정의된 개념일 수도 있습니다.
따라서 전자 Spin에 대한 이해는 모든 전자기 체계에 이해가 될 것입니다.
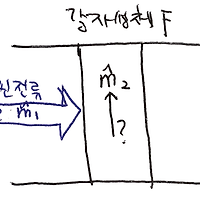
사실 자기장의 변화로 전류가 유도되는 것됩니다.
어떤 면적을 통과하는 자기장(자기선속)이 시간에 따라 변화할 때 전류, 즉 전압이 유도되는 현상을 발견한 패러데이의 이름을 딴 법칙입니다.
굳이 전류로 생각한다면 도선 내부의 전자가 가속해 외부에 가만히 있는 전자가 상대론적으로 힘을 받는 다고 생각하면 됩니다.
먼저 자기선속은 정의그대로
으로 표현 가능하고, 패러데이 유도법칙은
기전력
입니다. 이 법칙으로 폐회로의 전자기 유도와 같은 다양한 현상을 계산가능하지만 검색해도 간단히 나오므로 생략하겠습니다.
자화되지 않은 물질들은 thermal agitation에 의해 차가워진다면 lineup되어 자성을 띄기도 하며, 외부 자기장에의해 lineup된뒤 정렬된 자신의 자기장으로 자성의 성실이 남아있기도 하는데 이에 대한 내용은
magnetic material_AFM(antiferromagnetic), FM(ferromagnetic), paramagnetic, diamagnetic 에서 자세하게 다루겠습니다.
마지막으로 실제 자기장이 존재할때 통과 매체(공기, 물 등등)에 따라 어느정도 변동이 있을 수 있습니다. 이를 고려하는 것을
투과율(permeability) 라 하고 진공의 경우
입니다.
또한 위에서 고려한 물질 자체에서 나오는 자기장에 대한 상수를 라 한다면(magnetic material_AFM(antiferromagnetic), FM(ferromagnetic), paramagnetic, diamagnetic에서 자세히 다루겠습니다)
입니다.
정자기 에너지를 조금더 표현하자면,
자기 쌍극자(magnetic dipole)의 상호작용에 의해 발생하여
이고 이 자기장 식에서 첫 항은 부피전하(magnetic volume charge), 두번째항은 자기 표면 전하(magnetic surface charge)입니다. 또한 은 표면에 수지한 단위벡터입니다.
외부자기장에 의해 발생하는 에너지(Zeeman energy)는 다음과 같습니다.
여기서 H는 무엇이고 B는 무엇일까요??
이는 자석을 기준으로 나눌 수 있습니다.
결론 부터 말하자면 두개 모두 자기장을 의미하는 용어이고
B는 실제 자연에서 보이는 자기장(flux density)이고, H는 field strength로 자석의 N극에서 S극으로 향하는 장의 힘을 인위적으로 정의한 개념입니다.
이해를 하자면 다음그림을 보면 간단해집니다.
즉 자석 바깥의 장에 대해서는 H와 B는 같은 의미 입니다.
그러나 자석 내부에서는 B와 H의 방향이 다르며, B는 모든곳에서 continuous하고 H는 discontinuous합니다. 즉 H는 concept idea입니다. 이때 실제로 H는 자석 내부에서 demagnetization field로 후에 anisotropy자석을 이해하는데 엄청 중요합니다.
앞서 잠시 SI 단위계에 대해 말씀드렸는데, 자기장을 정의하는 방법이 전류냐, 자석 자체이냐에 따라 단위계가 나뉩니다.
전류로 정의한다면 SI 단위계이고, 자석이면 CGS 단위계 입니다.
SI로 자성의 량을 나타내는 척도인 자기 모멘트(Magnetic moment)를 나타낸다면, 면적 x 전류이고 단위는 [A/m2]입니다. 또한 자기장을 표현할 때 지름이 1m인 원형 도선에서 1A의 전류를 흘렀을 때 도선 중간에서 나오는 자기장을 1 A/m로 정의 합니다. 즉 H=i/(2a)입니다.
CGS는 magnetic pole을 가정하여 설명합니다. 쉽게 말하면, 전자와 같은 자기 입자를 기준으로 설명합니다.
따라서 magnetic pole의 값을 p라 정의한다면, magnetic moment는 m=pl 이고, 1g의 magnetic pole이 1cm/s2의 가속도의 힘을 받을 때를 1 emu로 정의합니다.
따라서 아까 zeeman energy도 E=-mH가 erg=emu * Oe 단위로 볼수 있습니다.
다음은 자기에서 사용되는 기호입니다.
'스핀트로닉스' 카테고리의 다른 글
| interlayer magnetic coupling (층간교환상호작용) (1) | 2018.02.01 |
|---|---|
| 스핀벨브 (spin valve) (2) | 2018.02.01 |
| 거대자기저항(GMR) (0) | 2018.01.22 |
| spin-transfer torque (STT) (0) | 2018.01.14 |
| Exchange bias (0) | 2018.01.13 |