↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
자기장(magnetic field)_비오-샤바르법칙(Biot Savart Law)_자석_패러데이 유도법칙 에서 물질 내의 전자들의 spin 덕에 자성을 띄는 물질이 존재한다고 포스팅 했습니다.
물질의 자기장이 절대 변화하지 않는 고유한 특성이면 좋겠지만, 물질 내부의 자기는 외부 자기장에 의해 크게 변화 합니다.
이 변화하는 정도에 따라 물질의 자성은 어러가지로 분류됩니다.
다음과 같은 그래프를 보겠습니다.
즉 앞서 전개한 식
$$\vec B=(1+\chi_0)\vec H=\vec H+4\pi \vec M$$
에서 mangetic susceptibility
$$\chi=\frac{M}{H}~or~\frac{\partial M}{\partial H}$$
가 이 물질에 외부 자기장에 반응하는 정도인데, 위 그래프에서 H가 외부 자기장이고 B가 물질내부에 변화하는 자기장 입니다.
위 그래프에서도 확실하게 보이지만, 정의 자체는
susceptibility가 약한것을 Diamagnetism, paramagnetism이라 하고 이때 susceptibility가 음수이면, dia, 양수이면, para입니다. 또한 강한것엔 ferromagnetism, antiferromagnetism이 있는데, H가 없을때 M이 0이 아닌것을 ferro, 항상 M이 0인것을 antiferro라 합니다. 추가로 susceptibility가 강한것은 자화의 배열이 long range로 정렬되어서 그럽니다. 특이하게 ferromagneticdl short range로 정렬되면 외부자기장에 의해 약하게 배열 되는데, 그것을 superparamagnetism이라 합니다. 이제 자세하게 보겠습니다.
가장 깔끔한 기준인 진공(vaccum)에서부터 시작해보겠습니다.
외부 자기장이 올라갈때마다 진공보다는 더 자기장이 증가하는 물질이 있습니다. 조금 증가하는 paramagnetic이라 이름 붙인 물질과 많이 증가하는 ferromagnetic(ferrimagnetic)이 있습니다.
이 물질 안의 원자의 전자들은 정말 외부 자기장에 맞춰 정렬되기 때문에 외부자기장에 의해 물질자체의 자기장이 생기게 됩니다.
이때 강자성체에 작용하는 자기장은 크게 네가지 성분이 있습니다.
교환자기장, 자기 이방성 자기장, 정자기 자기장, 외부자기장입니다.
이중 정자기 자기장과 외부자기장은 자기장(magnetic field)_비오-샤바르법칙(Biot Savart Law)_자석_패러데이 유도법칙에서 다룬 그대로 입니다.
본 포스팅에서는 이외의 것들을 적용한 것을 보겠습니다.
이때 스핀자체의 자기모멘트가 있는데 자기모멘트는
으로 정의할때
라 할 수 있습니다.(이때 g는 Lande g-factor로 고체 내의 전자는 2보다 약간 크고 분리되어있는 전자는 2.0023193이며, 는 Boh magneton입니다.)
또 외부 자기장이 증가함에 따라 진공보다는 덜 증가하는 물질도 있습니다.
이들을 diamagnetic이라 하는데 이들은 외부 자기장의 반대로 스핀이 정렬되어 물질내부에 반대 자기장이 생기게 됩니다.
사실 이들을 정의하는 것은 스핀의 상태로 정의합니다.
paramagentic의 경우 스핀중 한개나 두개가 unpaired된것을 의미합니다. 즉 주기율표에서 쉽게 찾을 수 있습니다.

diamagnetic은 모든 스핀이 pair인 것으로 unpaired 된 spin이 전혀 없는 간단하게는 He을 생각 할 수 있습니다. 이를 closed shell system이라 하고 이 때 재미있는 것은 [Ne] 3s1인 Na은 paramagnetic인데 ion이 되어 Na+가 되면 전자가 하나 줄어 diamagnetic입니다. 재미가 없다면 죄송합니다. 사실 거의 대부분의 물질이 diamagnetic이고 외부자기장과 반대로 자장이 생기는 것은 자기장(magnetic field)_비오-샤바르법칙(Biot Savart Law)_자석_패러데이 유도법칙에서 패러데이 유도 법칙 때문에 물질내에 유도 전류가 생겨 반대로 작용하는 것입니다.
사실 모든 물질은 이러한 성질이 있지만, 다른 물질, paramagnetic이나 ferromagntiec 같은 경우 스핀으로 유도되는 자기장이 너무 강해 이러한 성질이 무시됩니다.
더 깊게 들여다 본다면, 자기장 내에서 자유전자는 Larmor precession이라는 것을 하고, 물질에 가해지는 외부자기장에의한 에너지를 Zeeman energy (지만 에너지)라 한다면
$$E=\mu_B H,~~\mu_B=\frac{e\hbar}{2m_c}\rightarrow \omega=\frac{eH}{2m_c}$$로 angluar frequency가 도출됩니다. 따라서 전체 전자의 전하를 Z라 하면
$$I=-\frac{Ze\omega}{2\pi}$$
로 전류가 도출되며 이제 이 전류가 만드는 자기장을 구할 수 있는데 궤도의 단면적을 rho라 한다면,
$$m=IA=\pi<\rho^2>I,~~<\rho^2>=<x^2>+<y^2>=2<x^2>$$
입니다. 물론 삼차원일 경우를 가정하여 susceptibility까지 계산한다면,
$$<r^2>=<x^2>+<y^2>+<z^2>=3<x^2>\rightarrow~<\rho^2>=\frac{2}{3}<r^2>$$
이때 전자 한개당 m의 자기장으 유도하므로 전자 밀도 n을 정의하여
$$\chi=\frac{M}{H}=-\frac{n_a m }{H}=-\frac{n_a}{H}\pi(\frac{2}{3}<r^2>)\frac{Ze}{2\pi}\frac{eH}{2m_c}$$
$$=-\frac{\mu_0Ze^2n_a}{6m_c}$$

paramagnetic같은 경우 외부 자기장이 없다면 각 원자마다 spin 자기장은 있지만 무질서하게 배열되어 서로 상쇄되는 효과 때문에 전체 자기 모멘트는 0이 됩니다.
그러다가 외부 자기장이 걸리게 되면 정렬되는데 이 정렬되는 방향은 다음과 같이 생각하면 됩니다.
어떤 자석 가까이에 다른 자석을 가져다 놓으면 N극은 S극을 끌어당기고 N극은 밀어냅니다. 즉 가져다 놓은 자석과 같은 방향으로 자석이 배열되게 됩니다.
이러한 것과 같이 스핀을 자석이라 생각하면 외부 자기장과 같은 방향으로 배열됩니다.
다만 온도가 높아진다면 물질내의 분자간의 충돌 때문에 자기 모멘트의 정렬이 파괴되어 자화는 점점 감소합니다.
이런 물질구조로는 바로 insulator가 있습니다. 앞서 언급했듯 Spin들이 Localized되어있어야 하기 때문이기 때문에, 전자의 운동효과가 무시될 수 있는 자유전자가 없는 insulator에서 이런 경향이 많이 보입니다. 따라서 spin들이 옆의 spin들과 상호작용을 하지 않고 단지 superposition만 되어야 합니다.
즉 외부 자기장에 대해 물질 내부 spin들의 여러가지 방향의 평균값을 구하는데 여기서 ns를 spin의 갯수/unit volume이라는 정의를 가지고 계산을 진행한다면
$$u=-\vec m\cdot \vec H=-mHcos\theta$$
$$<cos\theta>=\frac{\int _{4\pi}e^{-u/kT}cos\theta d\Omega}{\int _{4\pi}e^{-u/kT}d\Omega}$$
$$\vec M =n_sm<cos\theta>$$
$$d\Omega =sin\theta d\theta\phi$$
$$<cos\theta>=\frac{\int _{0}^\pi e^{-mHcos\theta/kT}cos\theta sin\theta d\theta}{\int _{0}^\pi e^{-mHcos\theta/kT} sin\theta d\theta}$$
$$z=cos\theta,~x=\frac{mH}{kT} \rightarrow <cos\theta >=\frac{\int_{-1}^{1}e^{zx}zdz}{\int_{-1}^{1}e^{zx}dz}=\frac{d}{dx}ln~ e^{zx}dz$$
이후 적분에 대한 여러가지 수식을 화려하게 정리한다면
$$<cos\theta>=ctanh(x)-\frac{1}{x}=L(x)$$
입니다. 이때 x가 무한대가 되면 L(x)는 1이 되는데, 이것은 H가 무한대가 되거나, T가 0이 되는 즉 모든값이 align이 되는 상황입니다. 만약
$$x=\frac{mH}{kT}<<1$$이라면
$$<cos \theta>=\frac{1}{x}+\frac{x}{3}+\cdots -\frac{1}{x}\approx \frac{x}{3}$$으로 M에 대해 정리한다면,
$$M=n_sm\frac{1}{3}\frac{mH}{kT}=\frac{n_sm^2}{3kT}\vec H\Rightarrow \chi=\frac{M}{H}=\frac{n_sm^2}{3kT}=\frac{c}{T}$$
이때 c를 Curie constant라 합니다.
하지만, paramagnetism이라 하여 모두 절연체는 아닙니다. metal도 충분히 paramagnetism의 성질을 가질 수 있는데, 이를 Pauli paramagnetism이라 합니다.

왼쪽 그림과 같이 외부자기장이 없는 경우 fermi surface부근에서 외부자기장의 영향을 받지 않아 들뜨지 않습니다. 하지만, 외부 자기장이 있는 경우 에너지가 달라지는데, 바로 오른쪽 그림과 같이 외부 자기장과 같은 방향의 spin의 에너지는 높아지고 반대는 낮아지게 됩니다.(각각 다른 spin의 띠입니다.) 이때 이들은 metal이므로 Fermi level에 존재하는 만큼만 자성에 가미하게 됩니다. 따라서 기존 paramagnetism식에서 T/TF를 곱해 비율만 계산해 주면 됩니다.
$$\chi=\frac{n\mu_B^2}{3k_B}\frac{1}{T}\frac{T}{T_F}=\frac{n\mu_B^2}{3k_BT_F}$$로 결과식으로는 susceptiblity는 작고 신기하게 온도 의존성이 없는 것으로 나옵니다.(TF는 10000도 정도 됩니다.) 다시말해 paramagnet은 온도에 민감하고, conductor는 둔감하다고 보면 됩니다. 또한 각 스핀전자의 갯수에 따라 자성이 결정되므로, 각각의 스핀 전자의 밀도를 구하면 됩니다.
$$n_\uparrow = \frac{1}{2}\int_{-\mu_B}^\infty (f(E)D(E)+\mu_BH) dE$$에서 두가지 근사가 가능한데,
$$\mu_B H << kT_F,~~D(E+\mu_B)\approx D(E)+\mu_BHD'(E)$$따라서
$$n_\uparrow \approx \frac{1}{2}\int_0^\infty f(E)D(E)dE+\frac{1}{2}\mu_BHD(E_F)$$입니다. 반대 스핀은 뒷 항의 부호만 다르므로
$$M=\mu_B(n_\uparrow-n_\downarrow)=\mu_B(\mu_BHD(E_F))$$
$$D(E_F)=\frac{3N}{2}E_F\rightarrow~~\vec M=(\frac{3\mu_B^2N}{2E_F})\vec H,~\chi=\frac{3\mu_B^2N}{2k_BT_F}\frac{1}{V}=3\mu_B^2\frac{D(E_F)}{V}$$
ferromagnetic는 외부 자기장이 없어도 영구 자화를 가진 것입니다. 물론 외부 자기장에 영향을 받지만 외부자기장이 없을때도 물질내에서 자기장이 나타나는 특징이 있는 것입니다.
그렇다면 왜 ferromagnetic은 paramagnetic과 diamagnetic과 다르게 영구자석을 갖게 되는 것일까요?
먼저 unpaired spin의 수가 많습니다.

위 그림과 같이 unpaired한 전자들끼리의 상호작용으로 가장 낮은 에너지를 가진 상태가 물질이 자기장을 갖게 되는 상태입니다.
이 에어지를 교환에너지라 하고 Eex라 표현하겠습니다.
인데 여기서 Je는 교환적분(exchange integral)으로 파동함수를 다양한 상호작용 위치에너지 항으로 적분한 것입니다.
대부분 고체는 Je가 음이고 강자성체는 Je가 양입니다. 이 크기는 원자 상호간 거이 r과 d궤도의 반경 rd에 관계하며 다음 그래프와 같습니다.

즉 S1과 S2가 전자의 스핀 각 모멘트인데, 이들이 평행해야 Eex 가 음으로 나와 에너지가 낮아집니다.
이는 지극히 수식적인 내용이므로 현상적으로 보자면 두전자의 스핀이 반대방향이라면 두 전자에 작용하는 정전기적 척력인 쿨룽힘이 작아지고 같은 방향이라면 커집니다. 따라서 같은 방향이어야 에너지가 더 낮습니다.
또한 Hund의 법칙과 Pauli 배타원리에 의해 스핀이 paired되기보다 다른 궤도에 체워지는게 에너지가 더 낮습니다.
따라서 강자성체는 스핀이 많을 뿐더러 스핀의 정렬이 평행하고 이 상태 자체가 에너지가 낮아 외부 자기장이 없어도 자성이 유지가 됩니다.
사실 현실에서는 crystal 구조에서 원자와 원자가 결합하여 자기 모멘트가 전체적으로 줄어들 수 있는데, 이를 없애기 위해 N이나, Cr이나 O를 집어넣어 Grain boundary를 크게하여 결합을 끊어 4mu를 다시 살려줄 수 있습니다.
이제 에너지 관점으로 수식적으로 살펴보겠습니다. 각 스핀에 대해 위에서 논의한 성질을 수식적으로 표현한다면
$$u=-2J\sum _{l=1}^N \vec S_l\cdot \vec S_{l+1}$$에서 이웃한 스핀만 생각하는 에너지와, 스핀의 자성에 대한 식을 정의할 수 있습니다.
$$u_l=-2J\vec S_l\cdot(\vec S_{l-1} +\vec S_{l+1}), ~\vec \mu_l=-g\mu_B \vec S_l,~\mu_B=-\frac{e\hbar}{2mc}$$
$$u_l=-\vec \mu_l[\frac{-2J}{g\mu_B}](\vec S_{l-1}+\vec S_{l+1})=-\vec \mu _l\cdot \vec B_{eff}$$
라 쓰고 여기서 B를 effctive field라 부릅니다. 이제부터 모든 강자성체에대한 성질에 이 effective field가 사용되게 됩니다. 더 자세하게 보기 위해 정리한다면
$$\vec B_{eff}=-\frac{2J}{g\mu_B}(\vec S_{l-1}+\vec S_{l+1})=\frac{2J}{g^2\mu^2_B}(\vec \mu_{l-1}+\vec \mu_{l+1})$$
$$\vec {B}_{eff}=<\vec B>=\frac{4J}{g^2\mu_B^2n}M$$
$$\vec M =n<\vec \mu>,~~\vec B_{eff}=\lambda \vec M$$
으로 스핀에 의한 자성이 이웃한 스핀에 외부자기장을 주어 외부자기장이 없어도 자서잉 유지되는 것입니다.
paramagnetic관점으로 본다면, 외부자기장이 인가되면 M이 생기고 M이 effective field를 만들고 이것땜에 M이 또생기고... 이런 과정이 연속하는 것입니다. 앞선 Paramagnetism에서도 다루었듯, susceptibility의 식을 M의 정의에 대입시킨다면
$$\chi_P=\frac{C}{T}\rightarrow~\vec M =\frac{C}{T}(\vec B+{ext}+\lambda\vec M)$$으로 윗 식을 대입시킬 수 있습니다.
$$\vec M(1-\frac{C}{T}\lambda)=\frac{C}{T}\vec B_{ext}$$
$$\vec M =\frac{C}{T}\frac{1}{1-C\lambda /T}B_{ext}$$로 온도가

$$T_c=C\lambda$$를 경계로 크면 paramagnetism을 작으면 ferromagnetism을 갖습니다. 사실 susceptibility의 정의도
$$\chi=\frac{C}{T-T_c}=\frac{M}{H},~in~general~\chi\sim (T-T_c)^\alpha,~\alpha=1/2$$
반강자성체(antiferromagnetic)은 어떻게 된걸까요??
위에서 했던 논의에서 원자간의 결합이 공유결합이라면, 인접한 전자의 스핀방향이 반대방향이어야 안정합니다.
즉 교환에너지에서 Je가 음수이기 때문에 다음그림과 같이 인접한 원자들의 자기 모멘트는 서로 반대 방향으로 정렬됩니다.
마지막으로 최근 가장 핫한 물질인 Ferrimagnet을 아주 간단하게 본다면(왜 핫한지, 이외 자세한 응용에 대해서는 Ferrimagnetism 응용을 참조해 주세요) 반 강자성체에서 서로 반대가 되는 스핀들이 다른 moment를 갖고 있기 때문에 아예 자성이 없는 것이 아니라 외부로 자성이 조금 나오는 것입니다. 이런 현상이 나오는 이유는 정말 이게 다이기 때문에 본 포스팅에서는 이정도만 다루겠습니다.
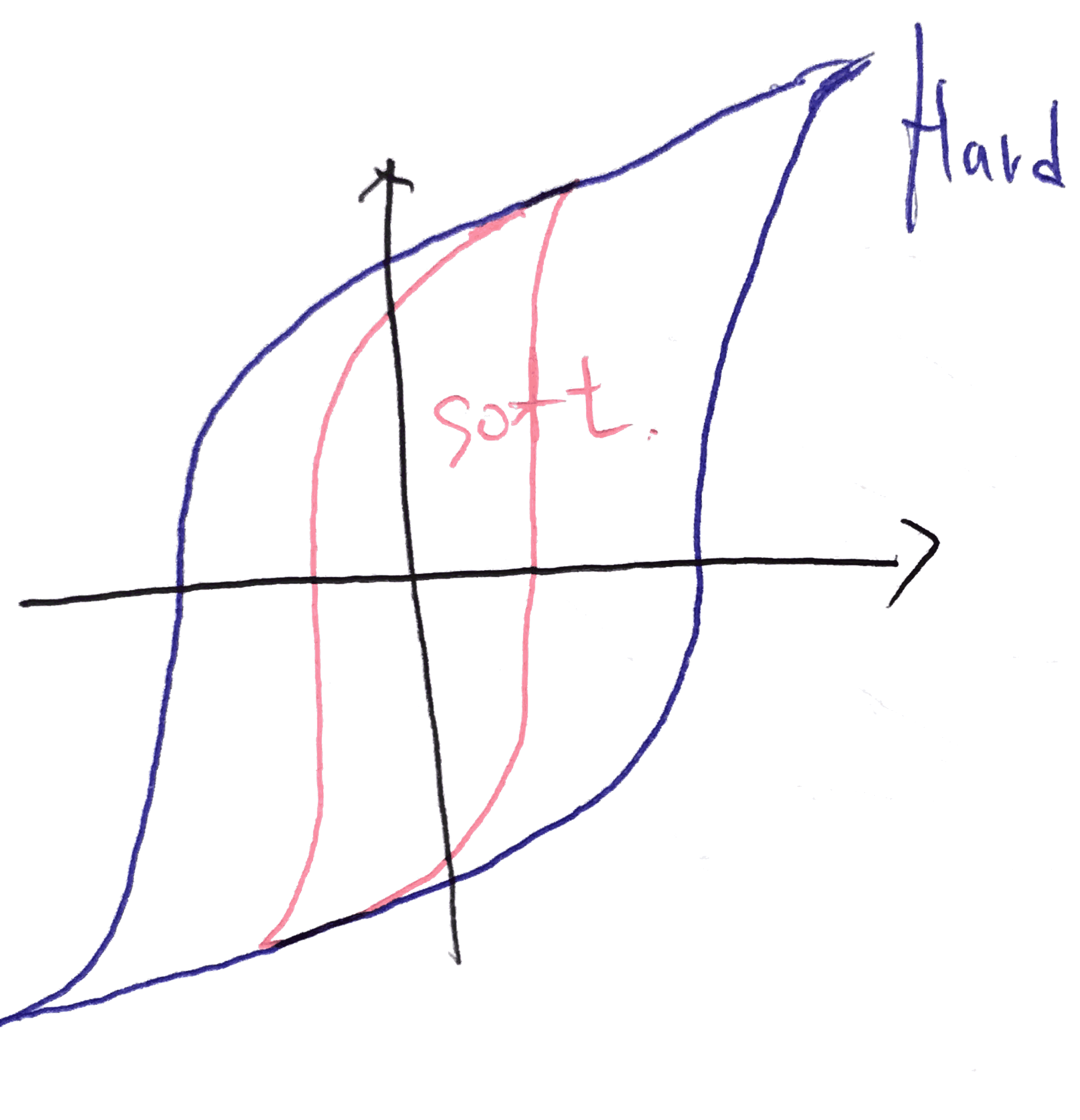
물질 자성은 자기장 B를 측정해서 구할 수 도 있는데 이 B는
이며 B로 측정했을때 그래프 내부의 넓이는 같은 힘의 제곱이므로 바뀌는 동안 사용된 에너지라 볼 수 있습니다.
이 그래프를 다시 0으로 바꾸고 싶다면 saturation되기전에 외부 자기장에 방향을 바꾸고 점점 줄여나가면 loop가 점점 작아져서 H=0이 됩니다.
또한 아래 그림과 같이 루프 면적이 큰것과 작은 것이 있는데, 큰것을 경질 작은 것을 연질재료라 합니다. 여기서 경질재료는 큰 보자력(coercive field)를 가지고 있습니다. 더 자세한 사항은 자기 이력곡선 (Hysteresis loop) _ 히스테리시스 곡선을 참조해 주세요!
이제 정리해 보겠습니다. 자성체에 존재하는 스핀이 받는 에너지는
즉 exchange energy + magnetocrystalline energy +demagnetization energy + Zeeman energy 로 구성되어있습니다. 이들을 모두 수직으로 구하여 더한다면(각각의 에너지에 대한 식은 이 포스팅 가장위에 "가정"에 링크되어 있습니다.)

이 스핀에 작용하는 모든 에너지를 종합하여 외부 Field H처럼 나타낸다면

입니다.
'스핀트로닉스' 카테고리의 다른 글
| Ferrimagnetism, Antiferromagnet 응용 (0) | 2019.06.08 |
|---|---|
| 스핀파(spin wave) _spin pumping, spin seebeck, magnon (4) | 2019.06.07 |
| Modular Approach to Spintronics (0) | 2019.05.13 |
| Pole and Current Model (0) | 2019.04.25 |
| 전자석 (0) | 2019.04.25 |




