| 정의상 가정 | 자성체(magnetic material)_강반자성체 AFM(antiferromagnetic), 강자성체 FM(ferromagnetic), paramagnetic, diamagnetic, 자화에너지 |
| 내용상 가정 | |
| 공식 | |
| 단위 | |
| 응용 |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
사실 Ferrimagnet은 Antiferromagnet을 직접 공부하는것이 어려워서 연구되어오는 물질이지만, 요즘 가장 Hot한 물질 구조입니다.
산화가 엄청 잘되고 전류가 흐를때 독특해서 잘 안쓰이지만,
사실 자연에서 자성체중에서는 가장 존재하는 양이 많습니다.(Ferri>Antiferro>Ferro)
예전에 일본에서 magnetic optic분야에서 상용화가 되었던 물질이기도 한 이 Ferrimagnet에 대해 알아보겠습니다.
Ferrimagnet을 만드는 물질이 바로 Rare Earth 물질인데, 대표적으로 Gd이 있습니다.
이 Gd의 4 f orbital이 transport에 관련하고, 5d가 Magnetization에 관여합니다.
Magnetic moment는 Fermilevel과 멀어서 직접 전도가 되지 않지만, 3d orbital과 hunt coupling을 하여(intra atomic exchange coupling)전도가 되며,
$$g=1-\frac{J(J+1)+L(L+1)-S(S+1)}{2}=2$$
입니다. 보통 Rare-earth (RE) - Transition Metal (TM)의 합으로 구성되는데,
서로 반대가 되는 RE와 TM은 서로 상쇄를 시키다가 조금더 우세한 쪽이 전체 net magnetic field가 생기는데,
TM은 exchange가 강해 온도에 덜 민감하고, RE는 exchange가 비교적 약한해 온도에 민감하여
온도를 변화시키다보면 net magnetization이 0이 되는 지점이 존재합니다.
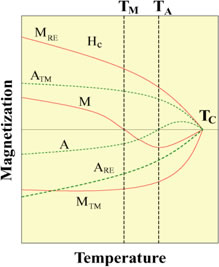
문제는 다음 그림처럼 두점이 존재한다는 것인데, 바로 Tm, Ta가 있습니다.
즉 Tm, magnetic moment가 0이 되는 지점과, Angular moment가 0이 되는 지점이 있습니다.
이 두점 중에 antiferromagnet의 정의인 net magnetic field가 0이 되는 지점은 바로 어디일까요?
그러기 위해 먼저 Angular moment와 magnetic moment의 차이를 알아야 합니다. 두 parameter사이의 관계는
$$\vec S=-\frac{\vec M}{\sigma}$$
입니다. 즉 RE와 TM의 S와 M의 정도가 달라 두 0이 되는 지점이 도출되 는 것입니다.
Angular moment는 실제로 계산하는 데만 쓰고 magnetic moment는 실제 관측에서 측정됩니다.
즉 angular moment의 경우
$$\frac{\partial \hat S}{\partial t}=\frac{1}{i\hbar}[\hat S,~\hat H]=\gamma \vec S \times \vec B_{ex}$$
$$=\gamma \vec \sigma \times \vec J\vec \sigma _1\vec \sigma_2$$
$$S=\vec S_{Gd}+\vec S_{Co}$$
으로 계산상에서만 존재합니다.
하지만 magnetic moment의 경우
$$\frac{\partial \vec M}{\partial t}=-|\gamma |\vec M \times \vec B$$
$$M=M_{Gd}+M_{Co}$$
인데, spin transport는 S로 진행되고, dynamics 관점에서는 S를 써야하기 때문에 Ta를 antiferromagnetic이라 봐야합니다.
Tm은 finite Zeeman coupling으로 M이 0이된 것으로
Ta는 antiferromagnet과 finite Zeeman coupling이 결합된 것입니다.
사실 다른이유로 다음과 같이 정의해야 antiferro의 Domain wall motion의 엄청난 속도와 같은 현상이 설명이 되기 때문입니다.
직관적으로는 다음 실험결과가 가장 잘 보여집니다.
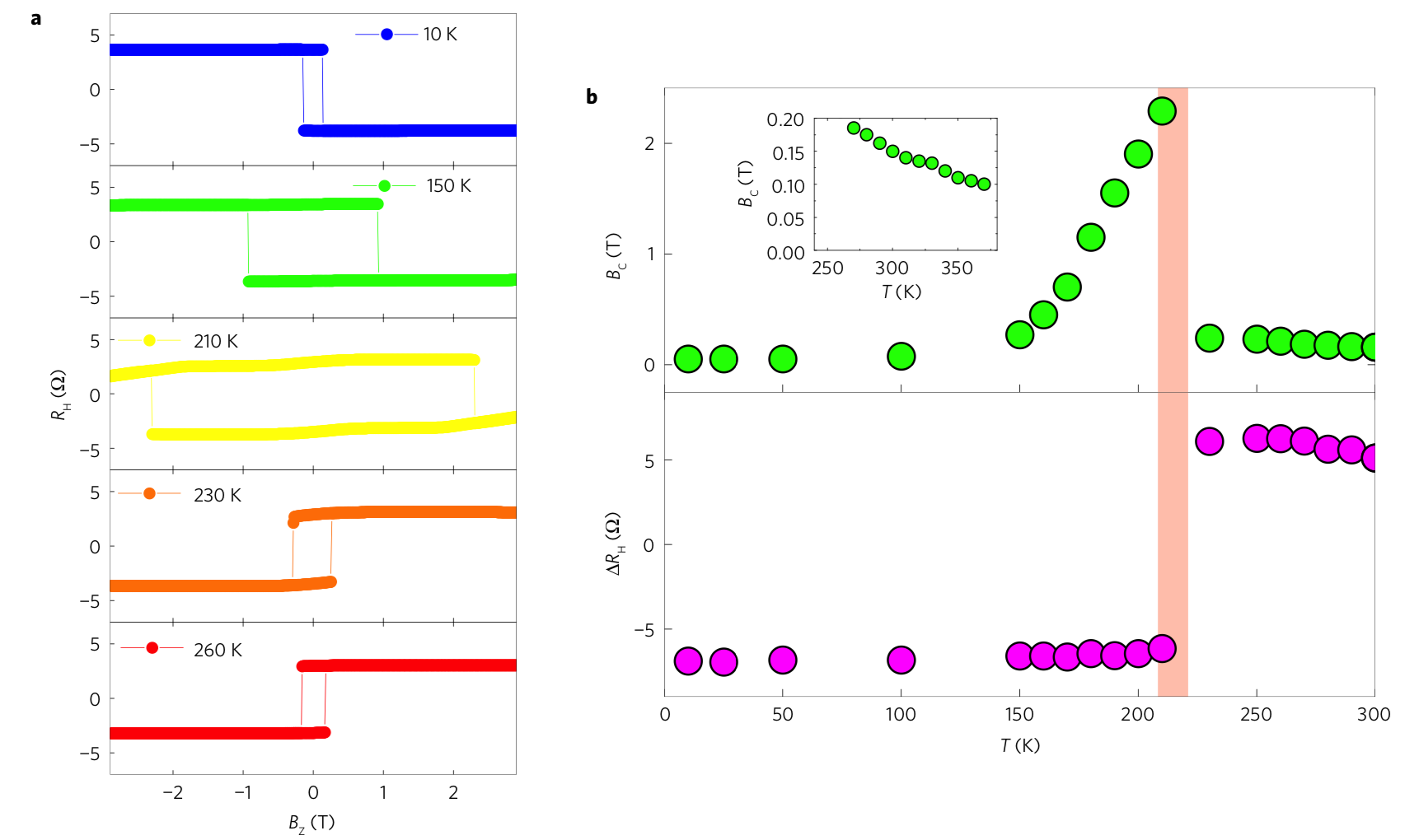
다음과 같이 온도에 따라 magnetization이 달라지게 되며 Tm에서 0이됩니다.
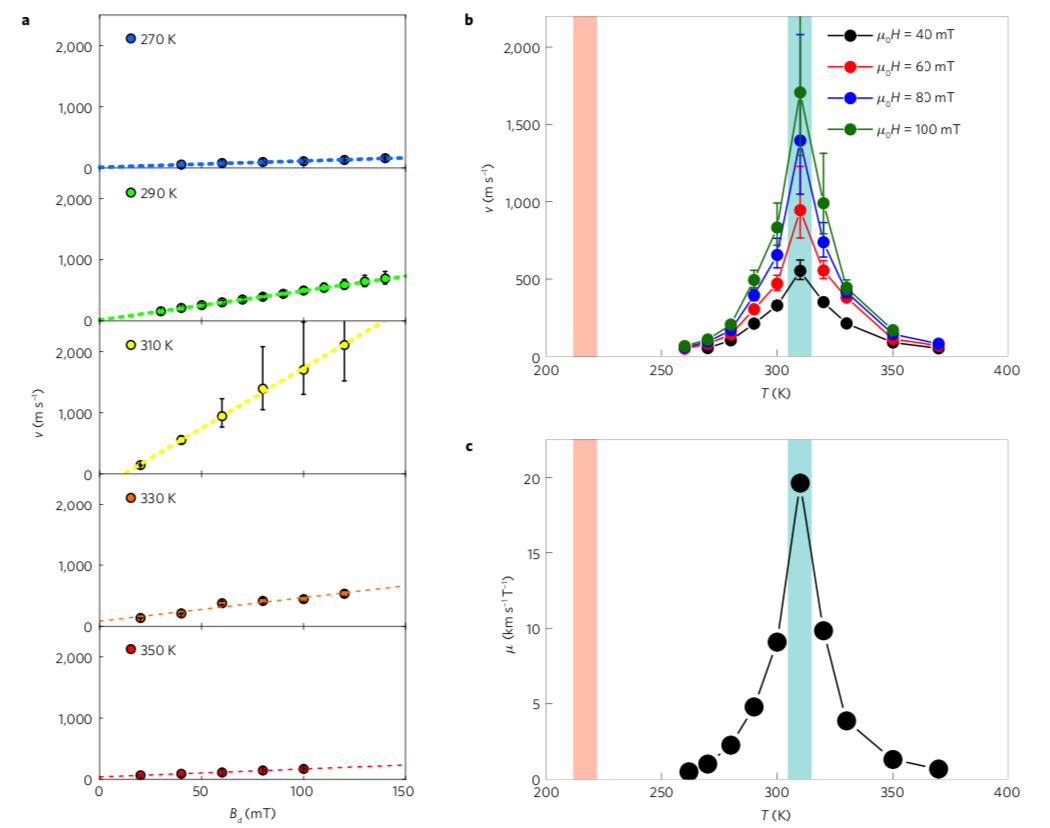
또한 domain velocity도 Ta에서 급격하게 커지게 됩니다.
최근에 너무나도 핫하기 때문에 반강자성체에대해 조금더 다루겠습니다.
지금까지 잘 알려저온 반 강자성체는
Fe-Mn, Ni-Mn, Pt-Mn, Ir-Mn 이 있습니다.
이중 disordered FCC인 Fe-Mn은 Neel temp이 낮아 (425~525 K) 잘 쓰이지 않으며 ordered fct인 Ni-Mn은 어중간한 포지션으로 또 잘 쓰이지 않습니다.
따라서 주로 Pt-Mn과 Ir-Mn이 쓰인느데, PtMn은 Mn이 41~66%정도 조성을 가지고, IrMn은 Ir이 14~31% 정도 조성을 가집니다.
초반에 Pt-Mn을 많이 썻는데, 이게 ordered fct이지만, neel temp이 975 K로 엄청 높아 좋았으나, 두껍게 쌓아야하고 Pt가 비쌌어서 Ir-Mn으로 바꿔 사용되기도 했습니다.
Ir-Mn은 disordered fcc이고 neel temp도 750 K정도로 얇은 두께에서도 나와 주로 사용되는가 싶었지만, Ir가격이 점점 비싸짐에 따라 Pt-Mn으로 바뀌었습니다.
이전까지는 주로 MTJ에 exchange bias를 가하기 위해 사용하였습니다.
'스핀트로닉스' 카테고리의 다른 글
| 자기 이방성 에너지(magnetic anisotropy energy) (9) | 2019.06.18 |
|---|---|
| ferromagnetic resonance (FMR)_magnetic resonance (0) | 2019.06.08 |
| 스핀파(spin wave) _spin pumping, spin seebeck, magnon (4) | 2019.06.07 |
| 자성체(magnetic material)_강반자성체 AFM(antiferromagnetic), 강자성체 FM(ferromagnetic), paramagnetic, diamagnetic, 자화에너지 (1) | 2019.06.07 |
| Modular Approach to Spintronics (0) | 2019.05.13 |



