|
정의상 가정 |
|
|
내용상 가정 |
angular momentum conservation과 energy conservation이 만족 |
|
공식 |
|
|
단위 |
|
|
응용 |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
spin-transfer torque는 말 그대로 spin이 자성물질을 통과하며 torque(힘)을 발생시킨다는 것입니다.
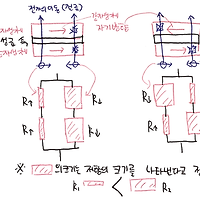
자성물질을 통과하는 것이므로 당연히 자기저항_거대자기저항(GMR) 원리가 나와야 합니다.
GMR은 자성체를 통과하는 전자 스핀이 자성체의 스핀방향이 같으면 scattering이 덜 일어나고 다르면 scattering이 많이 일어나 전도율이 변화한다는 원리였습니다.
여기서 하나 생각해 볼것은 위에서 scattering한 후 손실된 에너지는 어디로 가는가입니다.
spin dependent scattering(스핀 의존 산란)을 참조하면 이 때 scattering은 물리적으로 충돌하여 생기는 scattering이라기 보다, 통과하는 전자가 통과되는 자성체에 있던 스핀 배열과 상호작용하여 생기는 힘의 작용입니다.
따라서 당연히 전자 스핀이 힘을 받아 전도율이 감소할 때 기존의 자성체의 스핀도 작용반작용으로 영향을 받고 많은 전자스핀이 통과하면 통과되는 자성체의 스핀 배열이 영향을 받아 상대적 방향이 바뀌는 것 입니다.
즉 스핀 전류에 의해 스핀 전류가 통과하는 자성체의 스핀 배열이 변화한다는 것 입니다.
사실 스핀 전류의 계면에서 반사 투과 에너지밴드와 같은 것으로 설명하는 것이 있지만, 일딴 이렇게 보겠습니다.
수식적으로 얼마나 되는지 보기위해 위의 그림을 보겠습니다. 스핀 자화 단위가 인 스핀전류가 자화단위가
인 자성체를 통과한다면 자성체에 들어가는 전도전자 스핀 성분의 자성체 F의 자화방향과 평행한 성분(longitudinal spin component)는 두 벡터를 projection 한것과 같으므로
이고 수직한 성분(transverse spin component)는 수평한 성분을 뺴면 되므로
입니다. 이것은 벡터적으로 풀어쓰면
입니다.
이때 산란이 되기 위해선 수직한 방향 성분의 영향을 받을테니 통과할때 수평방향 성분의 차이를 보면 됩니다.
따라서 STT는 (F를 통과한 스핀전류의 수직항)-(F에 들어오는 스핀전류의 수직항)입니다. 이를 복잡하게 또는 실험적으로 계수를 계산한다면
이고 이때 방향은 입니다.
이때 P는 스핀분극률, J는 전하 전류 밀도 d는 자성체의 두께이고 이는 in-plane STT라 합니다.
여기까지가 STT를 GMR의 역으로 쉽게 해석해 놓은 설명이었습니다.
두가지 중요한 원리를 항상 만족해야하는데,
첫번쨰가 angular momentum conservation과 energy conservation이 만족해야한다는 것입니다. 또한 STT자체는 interace에서 scattering matrix와 transverse spin accumultion에 비례한다는 것입니다.
자성체에서 발생하는 원리는 스핀 필터(spin filter)에서 자세하게 기술해놓고 있습니다.
요약하자면 FM으로 spin polarized되는 spin 전류가 들어올때 들어오는 계면에서 spin이 filtering되면서 그 상호작용으로 에너지를 받아 flip되는 것입니다.
즉 이 STT는 3가지 component로 변화되는데,
입니다. 첫번째항은 uniform vector로 원래 있는 layer structure에서는 변화하지 않는 자성입니다.
두번째항은 spin transfer torque로 in-plane torque라고 불리기도 합니다. 왜냐하면 방향을 계산해 보면 plane 내부에서 형성되기 때문입니다. 이는 adiabatic하다고 합니다.
세번째항은 위에서도 설명했듯 perpendicular한 방향으로 생기는 out of plane torque라고도 불리는 torque입니다. 이때 σ가 field라 생각할 수 있고 실제 외부 자기장 field로 모사가능하므로 field like torque라고도 불립니다.
이는 non-adiabatic하다고 합니다.
in-plane STT에 수직한 out-of-plane STT(=field like STT= perpendicular STT)의 식과 설명도 있습니다.
추후 더 정확한 물리적 설명과 공식을 추가하겠습니다.
읽어주셔서 감사합니다!![]()
'스핀트로닉스' 카테고리의 다른 글
| interlayer magnetic coupling (층간교환상호작용) (0) | 2018.02.01 |
|---|---|
| 스핀벨브 (spin valve) (2) | 2018.02.01 |
| 거대자기저항(GMR) (0) | 2018.01.22 |
| 자기장(magnetic field)_비오-샤바르법칙(Biot Savart Law)_자석_패러데이 유도법칙 (6) | 2018.01.13 |
| Exchange bias (0) | 2018.01.13 |