|
정의상 가정 |
스핀세차운동토크(spin precession torque) magnetic material_강반자성AFM(antiferromagnetic), 강자성FM(ferromagnetic), paramagnetic, diamagnetic, 자화에너지 |
|
내용상 가정 |
|
|
공식 |

|
|
단위 |
|
|
응용 |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
자화방정식이라는 것은, 전자의 스핀이 어떠한 상태에 있는지, 어느정도에서 스핀 반전이 되는지 보는 운동 방정식입니다.
전자의 스핀이 존재한다면, 이웃한 스핀이 원인이든 격자모양의 원인이든 외부 자기장이 원인이든 스핀에 작용하는 자기장이 있을 것이고 스핀은 그 자기장과 상호작용을 하며, 아주 안정적인 경우 아래 그림과 같은 스핀세차운동토크(spin precession torque)인 스핀 세차운동을 하게 될것입니다.

입니다. 여기서 m은 spin이고 B는 외부 자기장입니다. 자세한 의미는 스핀세차운동토크(spin precession torque)를 클릭하세요!
여기서 모든 것이 정리되면 좋겠지만, 모든 회전(파동)이 그렇듯 안정한 상태도 있지만, 곧잘 발산이 되기도 하며 감쇠가 되기도 합니다.
감쇠란 산란에 의해 생기는 현상이지만, 본 system이 보존계이기 때문에 다른 system, 즉 다른 스핀이나 스핀파와 같은 에너지로 에너지가 빠저나가야 감쇠가 가능합니다.
사실 대부분의 에너지는 spin에서 orbital로, orbital에서 lattice로 가서 phonon과 같은 elastic에너지가 작용해 lattice에서 진동하여 소리나 열로 또는. angular momentum의 변화로(이때 angular momentum은 일정하므로, rigid body roatation이라 하여 샘플 자체가 돌거나 microscopic rotation이라하여 atom들이 회전합니다.)손실됩니다.
여기서는 모든 가능성을 한개로 퉁쳐서 감쇠의 가장 기본적인 식인, Rayleigh의 "dissipation function"으로 저항력이 속도에 비례한다는 식으로 정리하여 진행하겠습니다.
이때 는 어떤 물리량을 시간에 따라 미분한 값이고 η는 비례상수입니다.
이 system에서 실험적으로 감쇠가 온도에 크게 의존하여 감쇠가 산란현상의 결과물임을 가장하기 때문에 scattering time인 가 고려되어 자성을 시간에 미분한 속도와 같은 개념으로 생각할 수있습니다.
이때 물리량은 자성
입니다.
세차운동의 운동방정식에서 위 식을 대입하고 Lagrangian으로 Euler방정식을 정리한 뒤 유효자기장이 Zeeman energy (지만 에너지)임을 고려하여 증명하면(복잡한 증명을 한다면)

입니다. 이것이 바로 LLG방정식입니다.
감쇠에 의해 외부 유효자기장이 
과 수직하다는 것을 알 수 있습니다. 이때
으로 깔끔하게 정리한다면
입니다. 여기서 입니다.(이 기호는 intrinsic Gilbert Damping constant로 저항 계수라 생각 하면 됩니다. 좀더 직관적으로는 아래 그림의 빨간원의 갯수라고 생각하면 좋습니다.)
여기서부터 나오는 Heff에 대한 모든 기호의 원천을 알고 싶다면 magnetic material_강반자성AFM(antiferromagnetic), 강자성FM(ferromagnetic), paramagnetic, diamagnetic, 자화에너지 를 클릭해서 마지막 부분을 확인하세요!
이것이 바로 Damping torque입니다.
이때 감쇠에 의해 소실된 에너지는, system의 격자로 전달되어 스핀파(spin wave), 와전류(eddy current), lattice vibration, 변형등을 발생시키는데, 이는 스핀궤도 결합으로 발생합니다.

이후 전류가 흘러 spin-transfer torque (STT)나 spin orbit torque(SOT)와 같은 외부 torque가 존재한다면, 식에 spin torque(ST)에 대한 항이 추가가 되는데, 바로
입니다.
식의 의미를 좀더 보기 위해 먼저 spin-transfer torque (STT)을 참조하여 직접 STT식

을 대입해본다면

입니다.
이때 aj는 
먼저 Damping torque+Spin torque≠0일때는 perturbation이 일어나는데, 이때의 항을 구해보겠습니다.
윗 식을 정리하여 우변의

입니다. 이때 방향만 따져 를 수직방향 유효자기장 크기라 하고 방향에 대한 항을 식밖으로 뺀다면
에 따라 damping이 되거나 anti damping이 된다고 할 수 있습니다. 다시말해 윗 식의 첫번째항은 stable한 procession항으로 무시할 수 있고, 두번째 항이 이 spin의 momentum을 결정하는데 이것이 양수라면, damping이고, 음수라면 switching입니다.
aj는 positive이므로 α가 sign을 결정합니다.
이때 확실한 switching여부는 에너지로 알 수 있으므로, 한 주기 동안의 에너지를 보기위해 M에 H를 곱한다면,(p=(1,0,0)입니다.)

로 전류가 위와 같은 상황일때 swtching을 하게 됩니다. 즉 전류가 충분이 커지면 자화반전도 가능해집니다.
이를 anti-damping이라 합니다.
만약 가장 간단한 경우를 고려한다면 Damping torque+Spin torque=0인 상태 입니다. 즉

이라면, 두 항이 완벽하게 cancel out되어 윗 식에서

의 관계가 나오게 됩니다. 즉 이들의 해를 구한다면,

입니다. 이때 film으로만 구성되어있을때 Heff는 inplane의 demagnetization effect입니다.
이제 대충의 예제는 보았으니 ST에 대해서 일반화 해보겠습니다.
incident electron의 spin direction을 z방향이라 가정한다면(pinned layer의 magnetization direction) LLG equation은
이고 세번째 항이 inplane ST에 대한 항, 네번째 항이 perpendicular ST에 대한 항입니다. 이를 정리하면
로 perpendicular항은 단순히 field와 같은 field like torque가 되고 in plane은 damping과 같이 있는 STT가 되게 됩니다. 즉 in plane은 damping like torque입니다.
의미는 대충 알았으니 다시 표현해 보겠습니다.
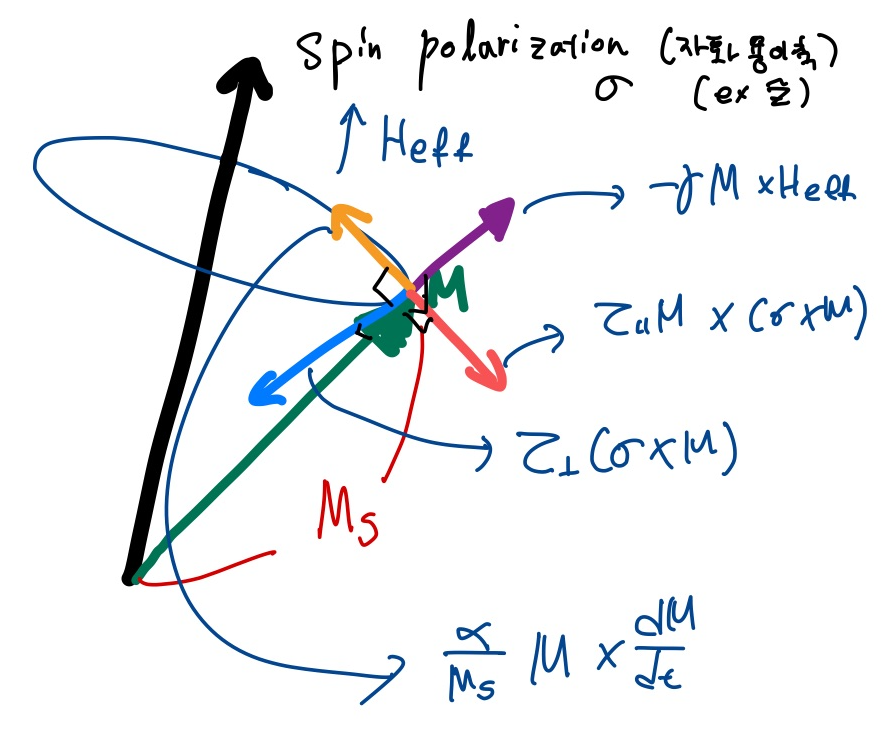
여기에서 첫 항을 보라색, 둘쨰 항을 주황색, 셋쨰 항을 빨간색, 넷째항을 하늘색이라 하면 다음 그림과 같고 각각 procession from effective field, damping torque, spin torque, anisotropy field라 합니다.
정확히 전류를 흐르는 상황을 가정해 보겠습니다. 그럼 먼저 H를 z방향이라 가정하고, aJ=aI라 하고 bJ=0이라 가정하겠습니다. 그러면으로 (αH+aI)이 <0일때 switching이 발생하고, >0이면 phonon과 같은 열에너지가 발생합니다.
이때 energy term을 구해본다면,

으로 energy는 dm/dt나 m x z에 연관되어있지않아. STT는 energy landscape에는 변화를 주지 않습니다. 다시말해 에너지 장벽을 바꾸지 않고 에너지 장벽보다 높은 에너지로 switching을 시킨다는 것입니다. 사실 에너지 장벽자체를 바꾸는 것은 외부 자기장 H에 의해 가능하다고 볼 수 있습니다.
따라서 STT자체는 H에 의한 항을 뛰어 넘어야 한고

입니다. 간단하게 첫 eta는 spin angular momentum per an electron이고, 두번쨰 분수는 magnetic moment갯수이고 세번째는 STT efficiency factor이고, 마지막 분수는 electron의 갯수입니다.
참고로 이때 thermal stability factor는

로 낮은 switching current와 높은 thermal stability factor를 가지기엔 겹치는 항이 있어 한계가 있으므로 이를 개선해야합니다.
이제spin orbit torque(SOT)가 spin torque일때를 계산해보겠습니다!
SOT는
ST항에 이 식을 대입시키면 됩니다. STT식과 비교해 볼때 앞의 상수는 aJ로 퉁칠 수 있더라도 뒤에 cross product가 하나 더있는것으로 보아 방향이 바뀌어야 합니다. Ferromanget의 기본 magnetization을 z축이라 할때 SOT는 y축이므로 모든걸 상수로 때려놓고 방향만 조정한다면,
다음 식에서 첫항은 가뿐히 무시하고 둘쨰항부터 본다면 둘쨰항의 첫항은 Damping입니다. 그러나 SOT는 damping을 이기고 switching을 한다는 개념보단 torque의 방향자체가 damping과는 관련없는 spin 방향자체를 눕힌다는 개념입니다, 따라서 세번 항이 spin orbit torque인데 아무리 이게 커도 절때 전체 항이 zero가 될 수 없습니다. 따라서 switching을 하려면 어쩔수 없이 외부 자기장이 필요합니다.
따라서 switching current도 STT와 달리

입니다. 즉 damping에 대한 항도 없고, 외부 자기장이 꼭 필요합니다.
이때 A는 MTJ cell area이고 A는 HM의 cross sectional area입니다.
추가로 정말 그냥 수식적으로만 유도한 general한 자성의 motion에 대한 식이라 하면
앞선 magnetic material_강반자성AFM(antiferromagnetic), 강자성FM(ferromagnetic), paramagnetic, diamagnetic, 자화에너지의 후반부에서 스핀에 작용하는 모든 에너지와 그 에너지를 자기장으로 치환한 effective field를 구해본적이 있습니다.
이를 자화의 움직임을 중점으로 전개한것이 운동방정식이라 할 수 있겠죠??
그 기본꼴은 바로

입니다.
추후 더 정확한 물리적 설명과 공식을 추가하겠습니다.
읽어주셔서 감사합니다!![]()
'스핀트로닉스' 카테고리의 다른 글
| Spin Hall Magnetoresistance (SMR) (0) | 2018.06.20 |
|---|---|
| 라쉬바 효과 (Rashba effect)_Shubnikov-de Haas oscillation (SdH oscillation) (0) | 2018.06.18 |
| 스핀세차운동토크(spin precession torque) (0) | 2018.06.17 |
| MOKE (Magneto-Optical Kerr Effect microscope) (0) | 2018.06.13 |
| 자기 이력곡선 (Hysteresis loop) _ 히스테리시스 곡선 (4) | 2018.05.24 |












