자화 반전 (magnetic switching) : field free switching

가정	[핵심] spin torque : field like torque VS damping like torque, [특집] STT vs SOT, [특집] Rashba vs Spin orbit torque, 라쉬바 효과 (Rashba effect)_Shubnikov-de Haas oscillation (SdH oscillation), [핵심] spin torque : field like torque VS damping like torque, 자화의 운동방정식(Landau-Lifshitz-Gilbert, LLG)_스핀 감쇠(spin damping)_ spin dynamics, 스핀세차운동토크(spin precession torque), spin-transfer torque (STT), spin orbit torque(SOT), 스핀 전류(spin current)_spin polarized current(스핀 분극 전류), two current model(이중 전류 모델), Ballistic spin transport, Diffusive spin transport
요약
응용

↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!

 

자성체에서 자화가 반전되는 것은 강유전체의 경우 자화의 운동방정식(Landau-Lifshitz-Gilbert, LLG)_스핀 감쇠(spin damping)_ spin dynamics의 원리를 따라갑니다. 다시말해 스핀을 가지고있는 자성체에 외부에서 어떤 방향의 스핀이 들어온다면 에너지 보존의 법칙에 의해 점점 방향이 바뀌다가 반대로 돌아가는 겁니다.

이때 반대라는 것은 자성체에서 에너지가 안정한 상태는 한 축을 기준으로 +방향과 -방향밖에 없기 때문입니다.

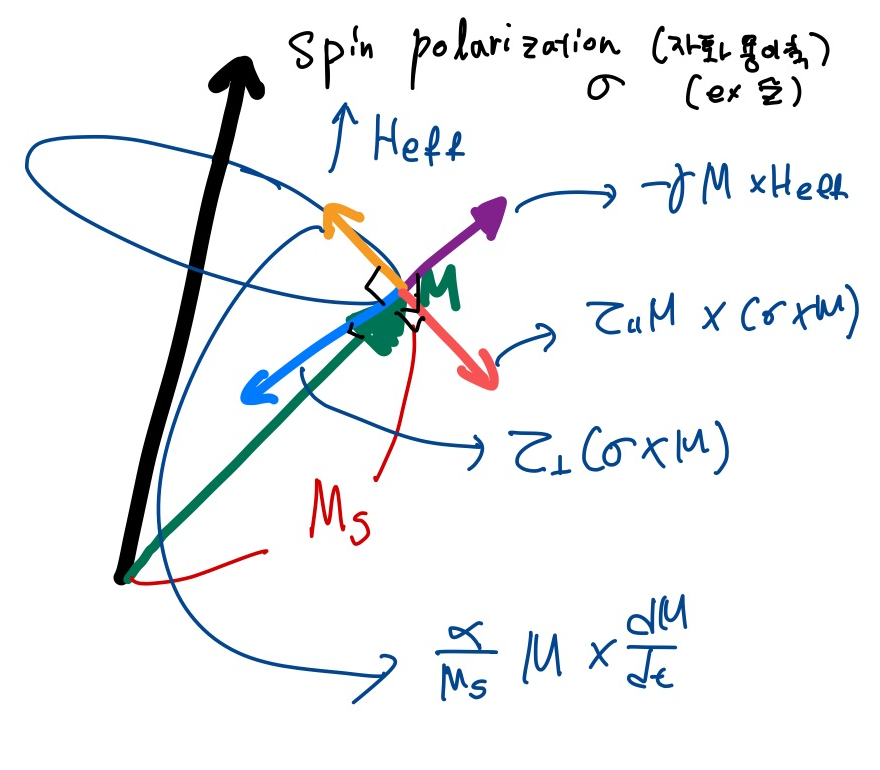
이들을 표현하는 LLG 방정식을 적어 놓고 본 포스팅을 시작하겠습니다.

$$\frac{dM}{dt}=-\gamma M \times H_{eff} +\frac{\alpha}{M_s}M\times \frac{dM}{dt}+\tau _{||}M\times (\sigma \times M)+\tau _{\perp} (\sigma \times M)$$

저희가 알고싶은 자화반전의 그 자화는 M입니다. 더 자세한 내용은 자화의 운동방정식(Landau-Lifshitz-Gilbert, LLG)_스핀 감쇠(spin damping)_ spin dynamics에 있지만 간략하게 상수들을 소개하자면 첫번째 항의 상수는 세차운동하는 회전수를 나타내는 Gyromagnetic ratio, alpha는 Damping factor로 자화가 엉뚱한 방향에 있을 때 얼마나 잘 에너지가 안정한 곳으로 오느냐를 나타내며, 뒤의 tau는 inplane과 out of plane의 torque입니다. 

여기서 M의 변화하는 정도를 torque라고 이름을 붙이는데 사실 원래 torque는 실제 작용하는 힘에 길이를 적분한 방향입니다. 그러나 여기서는 spin에 작용하는 힘 자체를 torque라고 이름 붙입니다.

마지막으로 sigma는 spin polarization입니다. 각 상수가 이해가 안되신다면 본 포스팅에서 모두 이해하실 수 있습니다. 첫항은 field torque, 둘째항은 damping torque입니다.

 

다시말해 자화반전시키는 방법은 Torque를 이용하는 것인데 이미 [핵심] spin torque : field like torque VS damping like torque포스팅에서 다루었습니다. 정리하자면 Torque는 지금까지 밝혀진바는 총 4가지

Spin Torque : Spin orbit coupling에 의해 Heavy Metal에서 생성된 스핀 전류가 Ferromagnet에 주입되며 생기는 Spin torque와 
Interfacial Torque : Spin orbit Scattering에 의해 Non magnet과 Ferromagnet사이에서 발생하는 Torque와
Orbital Torque : Non magnet에서 Orbital이 Ferromagnet에 주입하며 Orbital성분이 Spin으로 변환되는 Torque와
Anomalous Torque: Ferromagnet자체에서 Filtering과 같은 원리로 생성하는 Torque가 있습니다.

입니다. 앞의 포스팅에서는 엄청나게 단순하게 다루었지만, 본포스팅에서는 적용을 중점으로 다루겠습니다.

 

먼저 이미 상용화 되고 현재 산업에서 가장 활발하게 이용되는 Spin transfer torque(STT) 입니다. 원리는 터널 배리어를 사이에 두고 두개의 자성체가 붙어 있는데, 전류가 이 구조를 통과하면 첫번째 만나는 자성체 A를 거치며 전자에 스핀이 만들어지고(Spin polarization) 이 전자들이 두번째 자성체 B에 주입되어 상호작용하면서 자화반전이 이루어지는 것입니다. 

여기도 3가지 파트가 있는데 M의 방향의 vec m이라 한다면

$$\vec m , ~\vec  m \times (\vec m \times \vec \sigma),~\vec m \times \vec \sigma$$으로 첫번째 항은 자성체 B와 똑같은 방향의 스핀이 주입되는 것으로 원래 있는 것이므로 바뀌지 않습니다.

두번째가 익히 말하는 spin transfer torque로 Daming과 같은 방향으로 antidamping torque이라고도 불리고 in-plane torque이라고도 불리고 가끔씩 adiabatic torque이라고 불리기도 합니다. 이는 inplane을 가정하면

$$|\gamma | \frac{\hbar}{2e}\frac{PJ_e}{M_s d} \hat {m_2}\times (\hat {m_2} \times \hat {m_1})$$

으로 전류밀도 J와 스핀 분극률 P, 자성체의 두께 d입니다.

 

세번째 항은 익히 field like torque로 측정시 Field와 반대 혹은 같은 방향의 torque가 생겨 이런 이름을 붙입니다. 이는 non-adiabatic 한 torque이나 out of plane STT라 불리기도 합니다.

 

SOT의 경우에서도 anti damping torque를 이용하는데, 이는 STT에서 단순히 만들어진 Spin 전류의 원인이 바뀐것입니다.

즉 $$-|\gamma |\frac{\hbar}{2e}\frac{\theta _{SH}}{M_s d}\hat {m_2}\times [\hat {m_2}\times (\hat z \times \hat {J_N})]$$ 입니다. 즉 이는 SOT에 의해 만들어지는 스핀전류값이 매우 중요합니다.

 

그럼 Torque는 알겠는데 어느정도의 Torque가 가해져야 자화반전이 될까요??

 

바로 자화가 기본적으로 가지고 있던 Damping Torque을 이기는 Torque가 가해져야 합니다. 이외 Field like torque은 자화반전되는데 더 적은 전류나, 빠르게 반전시키기 위하게 도와주는 것이지, 선결조건은 Damping like torque입니다.

 

따라서 위 LLG 방정식에서 Dampling을 이기는 경우를 전류로 환산해 본다면 out of plane 시료에서

$$J_{sw}=\frac{2e}{\hbar}\mu_0 M_s t_{FM} \alpha (H_c +M_{eff}/2)/\xi_{DL}$$

이기서 alpha는 damping에 대한 상수, Meff는 demagnetization field, Hc는 in plane coercive field, 마지막항 xi는 spin torque efficiency입니다. 물론 속도나 안정도 관점에서 무조건 전류를 줄이도록 상수를 막 줄이는것이 좋진 않습니다. 한 예로 메모리의 성질을 나타내는 thermal stability factor는

$$\Delta = \frac{1}{2}M_sVH_c /k_B T$$ 으로 Hc가 작아지면 안정도도 줄어들게 됩니다.

참고로 SOT에서 Meff에 해당하는 demagnetization field는 Hc의 한 order정도 크기 때문에 J에 큰 영향을 미쳐서 thermal stability는 높이고 J는 낮추기 위해 demagnetization field를 엄청 낮추게 됩니다.

 

복잡하게 설명하였지만 단 두가지 식만 기억하시면 됩니다. 바로 

$$\vec{H_{eff}}=\vec{m}\times\vec P$$

$$\vec T=-\vec{m}\times \vec {H_{eff}}$$

 

그림으로 정리한다면 SOT가 작용했을때 effective field와 torque는 다음과 같이 주어지고 STT와 SOT도 비교하면 완전 같은 메커니즘으로 자화반전한다는 것을 알 수 있습니다.

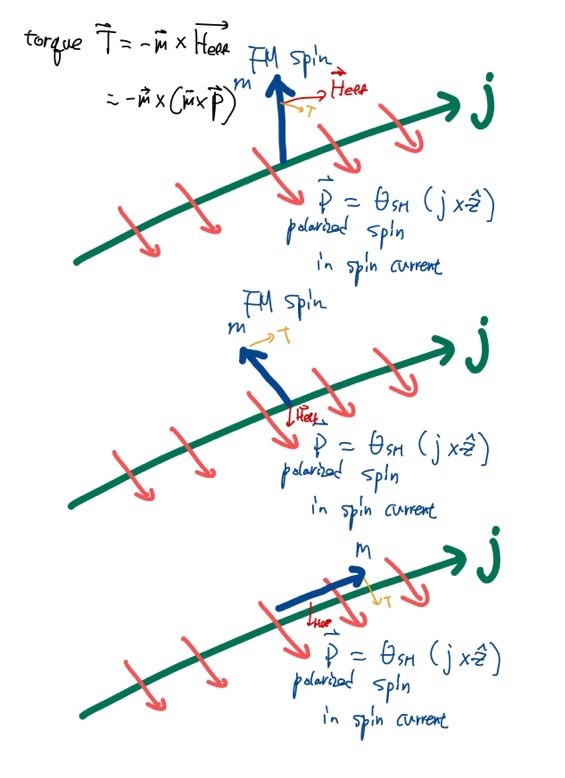
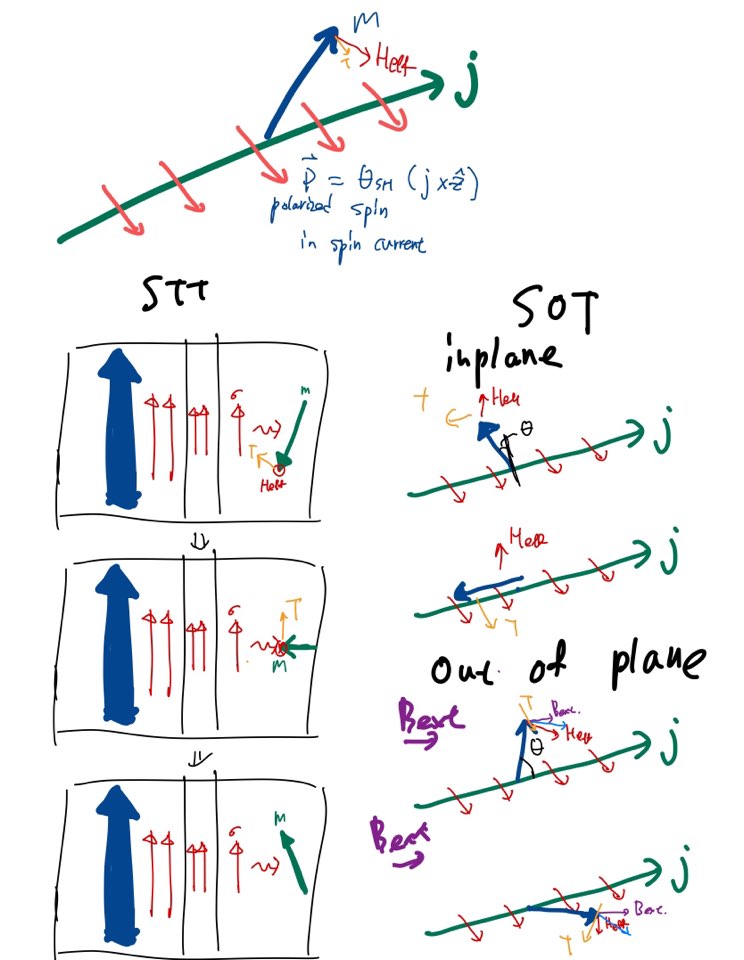
이외 이 자화반전을 쓸모있게 사용하기 위해서는 스핀전류가 만들어지는 효율이 중요합니다.

SOT의 경우 큰 Spin hall effect를 가지고 있는 물질을 사용해야합니다.

또한 쓸모있게 하기 위해서는 기술적인 문제도 있는데, Inplane이 아닌 out of plane의 자화를 SOT로 반전하기 위해서는 antidamping을 위해(다른 이유로 Dzyaloshinskii-Moriya interaction이 깨트려야합니다.) 외부 자기장이 필요한데, 외부자기장을 사용하지 않으려면 SOT 자성 박막의 아래층에 antiferromagnetic층이나 exchange coupling을 발생시킬 수 있는 층을 만듭니다.

 

외부자기장을 사용하지 않는 SOT 자화반전을 field free switching이라 합니다.

 

이렇게 한다면 직관적으로 볼때 유효자기장이 형성되어, 구조적으로 볼때 자성층의 symmetry를 breaking시킬 수 있습니다.

이 symmetry breaking을 위해 구조적으로 패턴의 외각에 기울기를 주어 breaking을 시킬 수 있습니다.

말로 설명이 잘 안되는데 궁금하신 분이 계시다면 https://doi.org/10.1073/pnas.1507474112을 참고하시길 바랍니다.

 

또한 다르게 생각해본다면, 자성층의 자화를 inplane도 아니고 out of plane이 이닌 상태로 틀어놓을 수 있습니다. 이들은 박막의 증착의 방향에 따라 조절 할 수 있는데, 이는 자기 이방성 에너지(magnetocrystalline anisotropy energy)의 bulk perpendicular anisotropy에서 다루겠습니다.

 

지금까지 논의한 바는 모두 한개의 spin의 자화반전에 대해서만 다루었는데, 실제는 magnetic domain에 대한 고려를 반드시 해야합니다.