전위(electric potential 전위차)

 정의상 가정

 전기장(electric field), 위치에너지

 내용상 가정

 가우스 법칙(Gauss's law)

 공식

     

 단위

 energy : [V]=[W]=[J]/ potential : [V]=[J/C]=Volt

 응용

 푸아송방정식(Poisson’s equation)/ 라플라스방정식((Laplace's equation)

↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!

전기력도 엄연한 힘이므로 에너지를 정의할 수 있습니다.

에너지에서 정의한 바와 같이 힘X이동거리가 에너지 이므로

전기에너지도 힘X이동거리가 됩니다.

이때 전하의 속도를 측정해야 운동에너지를 정의할 수 있으나,

실제적으로 사용하는건 위치에너지를 더 많이 사용하여 전기적 위치에너지, 즉 '전위'에 대해서만 따로 정의하게되었습니다.

왜 그렇게 전위만 따질까요?

전류라는 개념이 전하의 속도를 포함하고 운동에너지와 견줄수 있기 때문에

속도를 발생시키는 가능성인 전위만 따지게 됩니다.

이 위치에너지 즉 potential의 정의는 다음과 같습니다.

 여기에 (-)을 붙인 것은 초기값을 0이라 정의하여 값에 (-)를 붙였습니다.

이 전기 위치에너지에는 다양한 성질이 있습니다.

앞선 가우스 법칙(Gauss's law)에서 논한 전기장의 성질인

이므로 전기력은 보존력이라는 것을 알았습니다.

즉 경로에 관계없이 아무리 자유분방한 움직임을 한다해도

의 적분값은 potential의 처음과 끝의 차이라는 것입니다,

다음 potential차이를 수식으로 나타내면 다음과 같습니다.

마지막 줄에는 gradient의 정의를 쓴것입니다.

즉 표현 방법이 많아졌습니다.

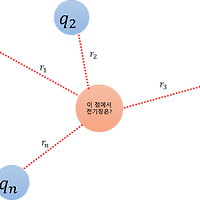
또한 superposition도 적용됩니다.

앞서 전기장에서 

이게 성립하였습니다.(전기장이 힘이니까 너무나도 당연합니다.)

그러나 이 전기장으로 전위를 계산할 때 단순한 적분관계로 분할될 수 있습니다. 

즉 입니다.