시간 독립적 슈뢰딩거 방정식(TIme-independent Srödinger equation)

정의상 가정	슈뢰딩거 방정식(Schrödinger equation) : 비상대론적, 푸리에 급수 energy eigenstate operator
내용상 가정	슈뢰딩거 방정식이 시간에 독립적이다. 은 0이 아니다. operator
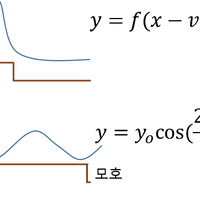
공식
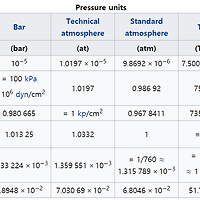
단위
응용	energy eigenstate

↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!

비상대론적 슈뢰딩거 방정식에서 시간에 독립하다는 것을 가정하고 풀어보겠습니다!!

시간에 독립적이라는 조건을 상정하는 순간 potential energy는 오직 거리에만 관련을 받습니다.

따라서

이고 이 방정식을 풀기 위해서는 변수 분리법을 이용해서 풀수 있습니다.

따라서 다음 식을 대입합니다.

그뒤 파동함수가 0이 아니라는 가정하에 양변으로 나누면 

이때 시간에 독립적이므로 좌변은 변화하지 않습니다. 즉 좌변은 constant입니다. 그럼 당연히 우변도 constant겠죠?? 이 constant를 E라 하겠습니다.

 이 constant를 이용해서 정리하면

이때 두번째 식의 경우 eigen value와 같은 형태입니다.

따라서 두번째 식을 만족하는 를 eigen value 라 하며

분리된 변수를 곱해 원래 파동함수를 나타내면 다음과 같습니다.

이때 선형 편미방 이므로 

해가와 라면

따라서 일반해는 

입니다.

여기서 만 구한다면 완벽한 일반해가 될것입니다.

을 구하는 방법은 일반해의 형태가 푸리에 급수와 같으므로 그 방법을 그대로 이용하면 됩니다.

구하기전에 알아야할 성질이 하나 있습니다. 바로 서로다른 두 파가 orthogonal하다는 것입니다.

이해가 안되는 성질은 앞선 energy eigenstate에서 증명하여 앞 링크를 잠시 참조하시길 바랍니다. 
참고로 아래 물결무늬 기호는 operator를 의미합니다.  왜 다음식이 전개되는지는 energy eigenstate에서의 약속입니다.

다시말해 

즉 델타함수로 orthogonal임을 알 수 있습니다.

그렇다면 을 계산한다면, 

초기값(initial condition)을 알아야 계산할 수 있습니다. 즉 t=0인 에서 

이 되게 됩니다.

이 파동함의 물리적 의미를 알아야할 필요가 있습니다.

먼저 time independent이므로 전체의 normalize가 성립해야합니다.

즉 영원히 같은 파동 밀도함수를 갖는 다는 것입니다.

이떄 위의 해를 이용한다면,

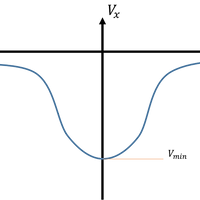
다음 모양의 확률밀도 함수를 갖게됩니다.

이때 맨 뒷항 real의 영향으로 모양이 위 아래로 요동칠수는 있습니다.

또한 x를 random variable로 하는 pdf가 independent하다는 의미는 기대값에도 영향을 미칩니다.

operator를 참조하여 기댓값을 써본다면

여기에 값을 대입해본다면, 시간에 대해 독립적임을 알 수 있습니다.

그렇다면 운동량의 기댓값은

다른 operator도 일반화 할 수 있습니다.

이 시간에 독립적이고

입니다.