|
정의상 가정 |
|
|
내용상 가정 |
|
|
공식 |
|
|
단위 |
|
|
응용 |
ReRAM (Redox Based Resistive Ram) 터널자기저항(tunnelling magnetoresistance, TMR) 스핀 의존 터널링(spin dependent tunneling, SDT) _spin polarization_tunneling spin polarization,TSP |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
Tunneling Current라는 것은 어떤 두 도체 사이에 부도체(insulator)가 있을 때 양쪽의 전자의 Wave Function이 중첩되어 마치 전자가 흐르는 형태가 되어 전류가 흐르는 것을 말합니다.
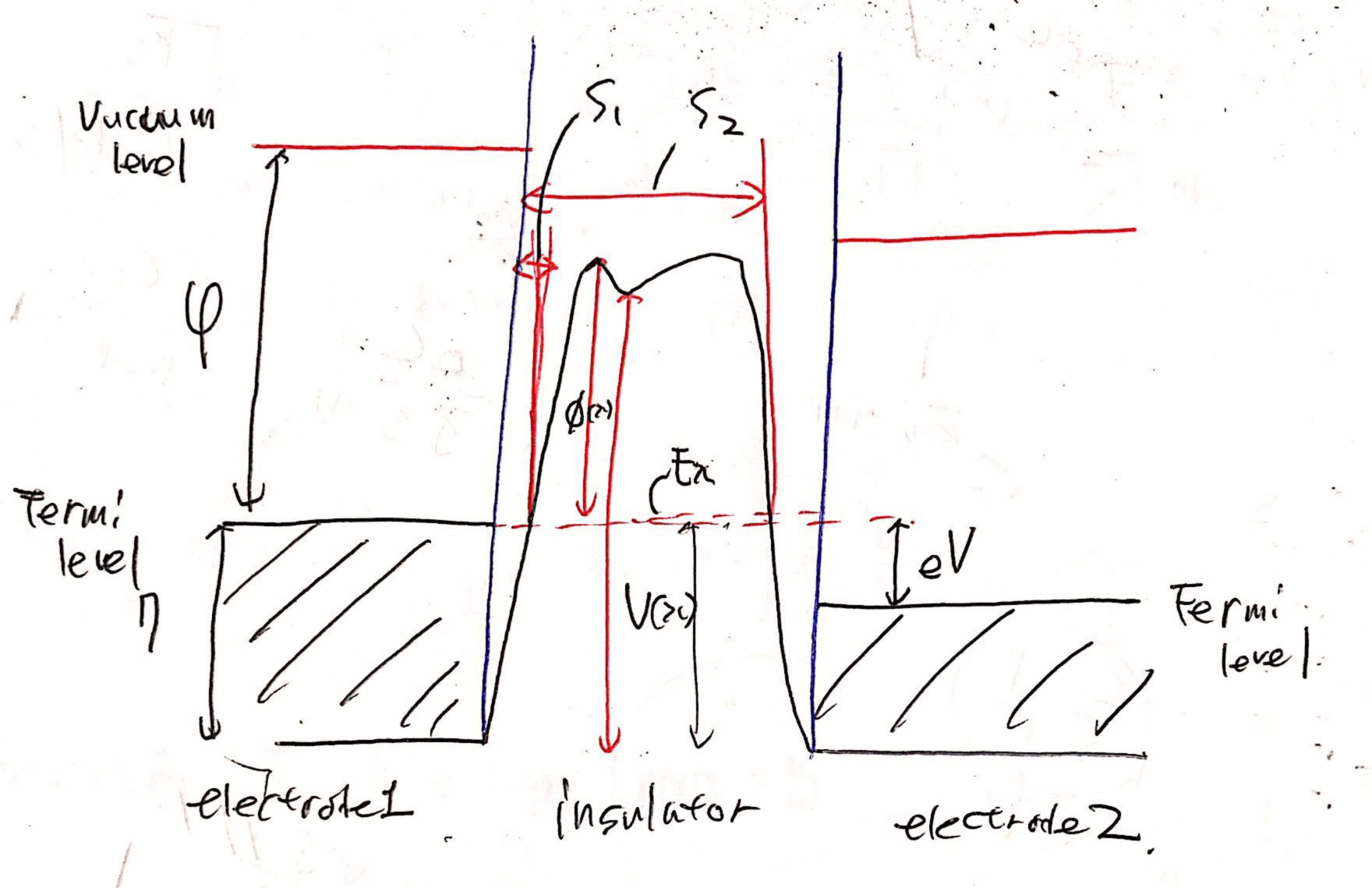
이러한 두 도체(혹은 반도체) 사이에 부도체가 있는 것을 물리학적으로 E가 양수인 Potential Wall이라 합니다. 이러한 상황의 특징은 그저 wave function이 잘 존재하고 wall이 존재하는 극단에 wave들이 연속성을 유지해야하므로, wave가 0으로 수렴해야한다는 것 입니다.
이전 포스팅에 다루었던 유도과정을 살짝 옅보자면

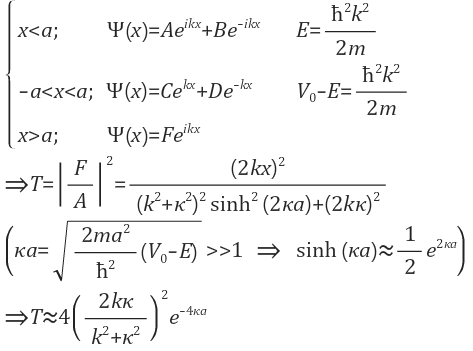
으로 대략 여러가지 파동함수들의 중첩으로 거리에 따라
$$e^{-4\kappa \alpha}$$
으로 감소하며 투과할 수 있다는 것입니다.
이를 근사하여 확률로 다시 표기한다면,
$$D(E_x) =exp\{-(4\pi)/(h) \int _{s_1}^{s_2}[2m(V(x)-E_x)]^{1/2}dx \}$$
입니다. 참고로 s_1은 potential wall이 ferimi level을 넘을 때의 위치고 s2는 wall이 potential wall 보다 감소할때의 거리입니다.(위쪽 그림에 표기되어있습니다.)
이제 확률을 알았으니 끝났습니다.
이제 확률로 전체 전자중 몇개가 갈수있는지 구하고, 이 갯수를 단위시간동안 생각한다면 전류가 됩니다.
확률식에 운좋게도 가해준 전압에 대한 식이 나와있으므로 논의는 전압 전류의 관계로 tunneling 저항도 구할 수 있습니다.
하나씩 천천히 구해보겠습니다.
먼저 확률을 알고있으므로 전자 밀도를 곱하면 됩니다. 여기선 전자를 입자로 생각하여 운동에너지의 속도로 생각해서
$$E_x=\frac{1}{2} m v_x^2$$을 대입하여 모든 속도에 따른 전자를 계산한다면
$$N_1 = \int_0^{v_m}v_xn(v_x)D(E_x)dv_x= \frac{1}{m} \int _0^{E_m}n(v_x)D(E_x) dE_x$$
이제 단위 부피당으로 생각하기 위해 Fermi Dirac Distribution function을 적용해 전자밀도를 구한다면
$$n(v)dv_xdv_ydv_z=\frac{2m^4}{h^3}f(E)dv_xdv_ydv_z$$
$$\Rightarrow n(v_x)=\frac{2m^4}{h^3}\int\int_{-\infty}^{\infty}f(E)dv_r$$
$$=\frac{4\pi m^3}{h^3}\int_0^{\infty}f(E)dE_r$$
여기까지 eletrode 1에서 eletrode 2로 넘어가는 전자의 갯수를 보았습니다.
이제 2에서 1로 넘어가는 전자의 갯수를 구해본다면, 다 똑같으나 Fermi level이 eV만큼 아래에 있으므로 E대신 E+eV를 사용하면 됩니다.
$$N_2=\frac{4\pi m^3}{h^3}\int_0^{\infty}f(E+eV)dE_r$$
따라서 넘어가는 총 전자갯수는
$$N=\int _0 ^{E_m}D(E_x)dE_x \times {\frac{4\pi m^2}{h^3}\int_0^{\infty}[f(E)-f(E+eV)]dE_r]}$$
입니다. 알아채셨을지 모르겠지만, 지금까지 시간에대한 차원이 들어있었습니다. 단위면적으로 계산한것이아닌 속도로 계산하여 시간으로 항상 나눈 상태였습니다. 따라서 위의 전자 갯수 N에 전하량 e를 곱하면 전류입니다.
$$J=\int _0 ^{E_m}D(E_x)dE_x \times {\frac{4\pi m^2e}{h^3}\int_0^{\infty}[f(E)-f(E+eV)]dE_r]}$$
이 식을 간단하게 하기위해
$$\xi_1=\frac{4 \pi m^2 e}{h^3}\int_0^\infty f(E) dE_r$$
$$\xi_2=\frac{4 \pi m^2 e}{h^3}\int_0^\infty f(E+eV) dE_r$$
로 정의하여
$$\xi=\xi_1-\xi_2$$
를 표기한다면 전류밀도는 간단하게
$$J=\int_0^{E_m}D(E_x)\xi dE_x$$
로 표기할 수 있습니다. 이제 그림에 적용하여 실제의 모든 파라미터를 적용한다면
$$D(E_x)=exp[-\frac{4\pi}{h}(2m)^{1/2}\int_{s_1}^{s_2}(\eta+\psi(x)-E_x)^{1/2}dx]$$
이고 이는 다음을 정의해서 쉽게 근사할 수 있습니다.
$$~~~\bar{\psi}=\frac{1}{\Delta S}\int_{s_1}^{s_2}\psi(x)dx, ~~A=(\frac{4\pi \beta \Delta s}{h})(2m)^{1/2}$$
$$\Rightarrow D(E_x)\approx exp[-A(\eta+\bar{\psi}-E_x)^{1/2}]$$
따라서 전류밀도 식에 바로 대입할수있는데, 여기서
$$\xi = \begin {pmatrix} (\frac{4\pi m e}{h^3}eV)&0<E_x<\eta-eV\\\frac{4\pi m e}{h^3}(\eta -E_x) & \eta-e <E_x<\eta\\ 0&E_x>\eta\end{pmatrix}$$
와 같이 구간을 나눌수 있습니다. 따라서 완성된 전류 밀도는
$$J=\frac{4\pi m e}{h^3}\{eV\int_0^{\eta-eV}exp[-A(\eta+\bar{\psi}-E_x)^{1/2}]dE_x+\int_{\eta-eV}^{\eta}exp[-A(\eta+\bar{\psi}-E_x)^{1/2}]dE_x\}$$
이제 수학적으로 잘 적분만 하면 됩니다. 적분을 잘 한다면
$$J=\frac{e}{2\pi h (\beta s)^2}\{(\psi-\frac{eV}{2}exp[-\frac{4\pi\beta s}{h}(2m)^{1/2}(\psi-\frac{eV}{2})]-(\psi+\frac{eV}{2}exp[-\frac{4\pi\beta s}{h}(2m)^{1/2}(\psi+\frac{eV}{2})])\}$$
입니다. 여기서 모르는 항이 바로 B인데, 이는 단순 상수로
$$\beta=1-(eV)^2/96(\psi_0+\eta-E_x-eV/2)^2$$
인데 식을 사용할수있는 범위인 $$0<V<\psi/e$$ 에서는 값이 변경되어도 오차율이 1%이내로 되기 때문에 B=1이라 가정합니다.
이제 실생활에서 식을 쓰기위해 Voltage와 전류의 식으로 만든다면 절연층의 두깨를 d, 가해준 전압을 V라 한다면,
$$J(V)=\frac{e}{2\pi h}\cdot \frac{1}{d^2}(\bar {\psi}-\frac{eV}{2})exp[-\frac{4\pi\sqrt{2m_e^*}}{h}\cdot d \cdot\sqrt{\bar{\psi}-\frac{eV}{2}}]-\frac{e}{2\pi h}\cdot \frac{1}{d^2}(\bar {\psi}+\frac{eV}{2})exp[-\frac{4\pi\sqrt{2m_e^*}}{h}\cdot d \cdot\sqrt{\bar{\psi}+\frac{eV}{2}}]$$
윗식은 에너지 단위 빼고 모두 MKS단위 입니다. 에너지의 경우 h가 6.626 070 040(81) × 10−34 J·s의 단위를 가지고 있고, eV는 1 eV = 1.60217646 × 10-19 J입니다. 따라서 eV로 통일시켜야하며 수식적으로 자릿수가 너무 많으므로 d를 nm단위로 사용하고, 유효 질량을 전자 질량과 같다고 근사한다면,
$$A=\frac{4\pi \sqrt{2m_e^*}}{h}=A_0\sqrt{\frac{m_e^*}{m_e}}~~eV^{-1/2}nm^{-1}$$
$$A_0=\frac{4\pi\sqrt{2m_e}}{h}=10.246~eV^{-1/2}nm^{-1}$$
$$C_0=\frac{e}{2\pi h}=6.166\times 10^8 ~eV^{-1}nm^2$$
로 상수를 정의한다 할때
$$J(V)=\frac{C_0}{d^2}(\bar{\psi}-\frac{eV}{2})exp[-A\cdot d\cdot \sqrt{\bar{\psi}-\frac{V}{2}}]-\frac{C_0}{d^2}(\bar{\psi}-\frac{eV}{2})exp[-A\cdot d\cdot \sqrt{\bar{\psi}+\frac{V}{2}}]$$
V에 직접가해준 V를 넣고 J를 측정한 I에 면적을 cm2단위로 나눠주면 됩니다. 다시말해
$$d~:~nm,~\psi~:~eV,~J~:~A/cm^2$$으로 실제 측정한 값과 잘 맞습니다.
그러나 박막이 조금만 두꺼워져도 잘 맞지 않습니다.
그 이유는 바로 두껍게 막을 증착하면 성질이 자꾸 바껴서 multi layer 절연층과 같은 효과를 보기 때문인데 이럴때는 다른 해결방법이 있습니다.
위 방법은 Simmons라는 분이 J. Appl. Phys. 34, 1793 (1963)라는 논문에서 제시한 방법으로 Barrier를 사이에 두고 흘러가는 conduction flux인 Fx와 양자역학적 Tunneling 확률을 구형의 Fermi sea전반에 걸처 적분한 값입니다.
$$J=e\int_0^{E_f}P(E_x)F_xdE_x$$
여기에 WKB 근사법을 차용하여,
$$P=exp[-2(\frac{2m}{\hbar^2})^{1/2}\int_0^d\sqrt{U(x)-E}dx]$$
윗 식을 전개하였지만, 이 식은 insulator 내부에 많은 차이가 있는 multilayer의 경우 가장 큰 barrier에 의해 current가 제안되기 때문에 적용이 되지 않습니다. 따라서 절연층 거리별 새로운 Barrier의 상태를 가정해서 더해야 합니다. 따라서
$$J(V)=(\sum_i{\frac{C_0}{(d/\Delta x_i)^2}(\bar{\psi}-\frac{eV}{2})})exp[-\sum_i{A\cdot d\cdot \sqrt{\bar{\psi}-\frac{V}{2}}}]-\frac{C_0}{d^2}(\bar{\psi}_i-\frac{eV}{2})exp[-A\cdot d\cdot \sqrt{\bar{\psi}+\frac{V}{2}}]$$
'전자공학' 카테고리의 다른 글
| 진공관 초고주파 신호 발생기 , 오실레이터 (GHz THz Signal Generation , oscillator) (0) | 2020.04.17 |
|---|---|
| 소자 전기 전자 계측, 측정 First Harmonics, Second Harmonics, Delta (0) | 2019.09.30 |
| Solder Reflow(솔더 리플로우) SMD (0) | 2019.08.01 |
| ReRAM (Redox Based Resistive Ram) (5) | 2019.06.22 |
| Thin Film Insulator_Capacitor(박막 커패시터) (2) | 2019.05.25 |



