|
정의상 가정 |
the finite square well_tunneling |
|
내용상 가정 |
|
|
공식 |
$$\varepsilon=\varepsilon_r \varepsilon_0$$ $$I=t^2\times ~~~~ J_0=\frac{e^2}{h^2}\frac{\sqrt{2mW_b-\frac{V_b}{2}}}{a}\cdot V_b ~~~~ \times ~~~~ P=exp(-\frac{2\sqrt{2m}}{\hbar}\cdot a \cdot \sqrt {W_b-\frac{V_b}{2}})$$ $$\Delta x \sim a_{min}=\frac{\hbar}{2\sqrt{2mW_b}}~(if,~\Delta p\geq \sqrt{2mW_b})$$ |
|
단위 |
$$\varepsilon_0=8.85\times 10^{-12}F/m$$ |
|
응용 |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
아주 오래전부터 메모리 소자나 반도체 소자에서는 얇은 박막의 커패시터를 엄청나게 많이 사용하였습니다.
사실 이 커패시터가 소자의 패러다임을 변화시키는데 핵심적인 key였습니다. 그 한 얘로 커패시터의 구조를 변화시킨 구조로 FINFET, V-NAND등이 있습니다.
Flash나 DRAM도 결국은 이 커패시터가 정보를 저장하는 부분이며
새로 발전하는 차세대 메모리도 이 insulator가 핵심인데,ReRAM과 FeRAM은 이 커패시터 자체가 핵심입니다.
이외 MRAM과 같은 소자에서도 thin film Insulator를 활발하게 도입합니다.
그렇다면 앞선 포스팅에서 자세하게 다루었던, 커패시터(Capacitor) _ Insulator (절연체)와는 어떤 차이가 있길래 얇은 박막 커패시터를 사용하는 것일까요?
가장 근본적인 이유는 두꺼운 커패시터의 경우 에칭공정을 할때 깊이 팔 수 가 없다는 것입니다.
두번째 이유로는 $$Q=CV=V\times k\frac{A}{l}$$이기 때문에 낮은 전압으로도 l이 낮다면 높은 전하량을 유도할 수 있다는 것입니다.
먼저 이 모든것을 이해하려면 Dielectric constant k를 이해해야합니다.
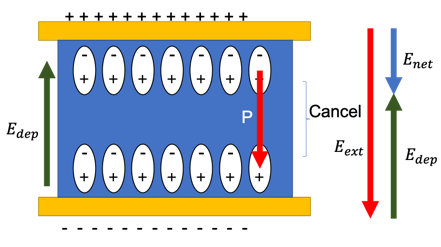
다음 그림을 보겠습니다. 다음과 같은 커패시터에 전압이 인가된다면, 내부의 원자들의 쌍극자 모멘트가 정렬됩니다. 따라서 외부 전기장을 Cancel out 시키는 방향으로 polarization P가 유도가 되고, 이를
$$P=\chi E$$라 합니다. 이떄 $$\chi ~:~Electric susceptibility $$는 Electric field에 대해 얼마나 dipole이 정렬이 되는지를 나타내는 항으로 이들이 정렬될때 내부 원자들 끼리는 Cancel이 되어 양 극에만 이 원자들의 전하가 남는데 이 전하때문에 생기는 전기장을 depolarization field라고 합니다. 즉 실제로 인가되는 전기장은$$\vec {E_{net}}=\vec{E_{ext}}-\vec{E_{dep}}$$인 net polarization입니다.
즉 두 극판사이에 5V를 걸었을 때 실제로는 2V정도만 걸리게 됩니다.
여기서 유도되는 전하량 Q는 두가지 전압으로 유도가 됩니다.
먼저 외부에서 걸어준 전압으로 유도가 되는 전하량 입니다. 이는 그냥 분극되는 유전체가 없다는 가정하에 유도되는 전하량이라 보면 되어 이 유도된 전하량은 이 전하량이 만들어내는 전기장이 외부에 의한 전기장과 같아질 때 까지 유도가 됩니다. 이때 이 전압이라 하면 External이 아니라 Net Voltage입니다.
다음으로 insulator의 분극에 의한 전압으로 유도가 되는 전하량인데, 분극에 의한 전하량은 외부에서 볼때는 분극의 극과 유도된 전하량의 합으로 보이므로 0으로 보입니다.
다시 위 net polarization field로 돌아가서, 지금 두 극판에는 분극에 의한 전하량이 유도가 되었고, net polarization field만큼인 2V만큼 전하량이 유도됩니다. 외부에서 볼때 두 극판에는 아직 외부 전기장과 같아질 만큼의 충분한 전하량이 쌓이지 않았으므로 전기장이 더 가해지게 됩니다. 그러면 더 많이 분극이 생기고 net field가 생기고 하는 과정에 의해 net field가 5V가 될때까지 더 많은 전하량이 유도가 됩니다.
다시말해 분극이 많이 존재할수록(Depolarization field가 더 많이 존재할 수록) 더 많은 량의 전하량 Q가 유도가 되는 것입니다.
따라서 같은 전압에서 더 많은 전하량을 얻고싶다면 Polarization을 높여야 하며, 이 polarization을 높이는 상수가 바로 electric susceptibility라 불리는 $$\chi$$입니다. 이는 외부 전기장에 의해 얼마나 polarization을 잘 시키냐하는 계수입니다.
여기에 또 중요하게 작용하는 계수가 있는데, 바로 permittivity $$\varepsilon=\varepsilon_r \varepsilon_0$$입니다.
이는 앞서 논의 하였던 것의 총집합이라 할 수 있는데, 외부 자기장에 반대로 dipole이 얼마나 생기는지 나타내는 계수로, 여기서 사용되는 relative permittivity는 dielectric constant와 같습니다.
$$\varepsilon_r=k=\chi_e+1$$
입니다.
전하량을 높게 유도해야하는 분야는 정말 많습니다. 크게 MOSFET이나 Flash와 같은 Gate Voltage로 동작시키는 분야인데, 그렇다면 단순히 이 $$\chi$$만 높은 물질만 찾으면 높은 전하량에 대한 문제는 끝이 날까요?
당연히 아닙니다!!
바로 insulator의 tunneling 문제가 있습니다. 즉 전하를 많이 유도했다 하더라도 Insulator자체의 Barrier가 낮아 leakage current가 줄줄 센다면 insulator로써의 역할과 전하를 유도하는 기능으로 문제가 많습니다.
| Material | Dielectric Constant k | Barrier Height, Wb(Si) | Effective Electron Mass, M* | a_min |
| SiO2 | 3.9 | 3.1 eV | 0.5m0 | 5.0 nm |
| Si3N4 | 7.6 | 2.4 eV | 0.43m0 | 6.0 nm |
| Al2O3 | 9 | 2.8 eV | 0.30m0 | 6.8 nm |
| HfO2 | 22 | 1.5 eV | 0.15m0 |
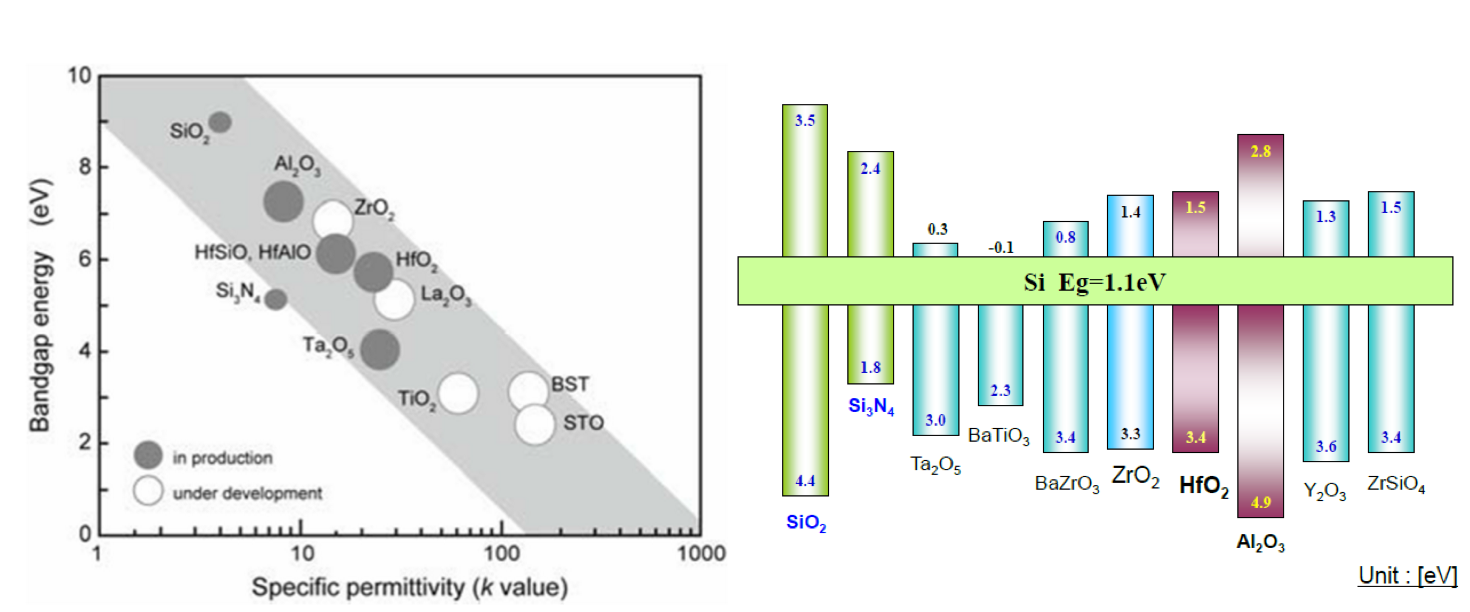
다음과 같이 아쉽게도 Dielectric Constant가 높아지면 Barrier Height가 감소하는 경향이 있습니다.
따라서 다음 그림을 살펴본다면, 이 작은 Barrier Height에 의해 tunneling이 많이 생길 수 있다는 것을 알 수 있습니다.
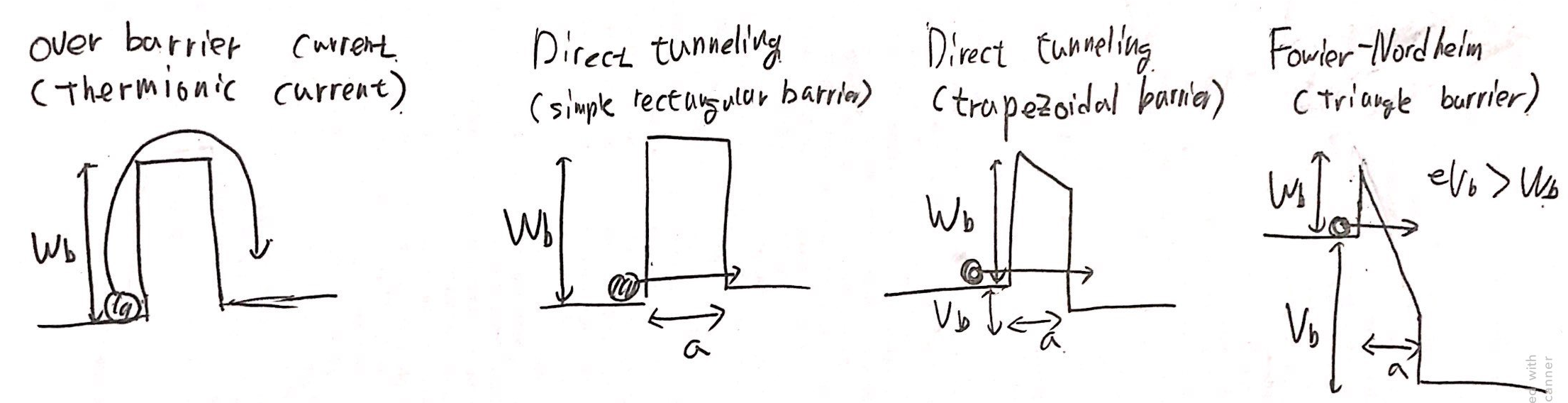
가장 왼쪽그림과 같이 단순히 열에의해 전자가 Barrier를 넘어가는 경우는 다음 식과 같이 별로 크지 않습니다.
$$I=t^2\times~~~~ J_0=\frac{4\pi emk^2_B}{h^3}r^2~~~~\times ~~~~ P=exp(-\frac{W_b}{k_BT})$$
그러나 Direct tunneling과 같은 경우 Vb가 0인 아무런 전압을 가하지 않은 상태에도 Barrier의 역할이 중요하게 됩니다.
$$I=t^2\times ~~~~ J_0=\frac{e^2}{h^2}\frac{\sqrt{2mW_b}}{a}\cdot V_b ~~~~ \times ~~~~ P=exp(-\frac{2\sqrt{2m}}{\hbar}\cdot a \cdot \sqrt {W_b})$$
왼쪽에서 세번째 그림처럼 Vb와 같은 전압(0<eVb<Wb)을 가해준다면, Barrier에 영향은 더 심각해집니다.
$$I=t^2\times ~~~~ J_0=\frac{e^2}{h^2}\frac{\sqrt{2m(W_b-\frac{V_b}{2})}}{a}\cdot V_b ~~~~ \times ~~~~ P=exp(-\frac{2\sqrt{2m}}{\hbar}\cdot a \cdot \sqrt {W_b-\frac{V_b}{2}})$$
마지막으로 전압을 Barrier보다 크게 가한다면,(eVb>Wb)
$$I=t^2 \times ~~~~ J_0=\frac{e^3}{8\pi h W_b}\cdot \frac{V_b^2}{a^2}~~~~ \times ~~~~P=exp(-\frac{2}{4} \cdot \frac{2\sqrt {2m}}{\hbar}\cdot a\cdot\frac{W_b^{3/2}}{eV_b})$$
요기서 끝이 아닙니다. Capacitance를 높이기 위해 무작정 Barrier의 거리 a를 좁혀도 문제가 되는게 있습니다.
바로 불확정성 원리(uncertainty principle)로 에너지 W x 시간 t = 운동량 P x 공간 I = Plank Constant라는 항상성립하는 이론이 적용이 됩니다. 다시말해 Heisenberg의 불확정성원리에 의해$$\Delta x \Delta p \geq \frac{\hbar}{2}$$로 전자의 불확정성인 위치 간격과 불확정적인 운동량을 고려한다면, 만약 Barrier의 거리가 이 전자의 불확정 위치 간격보다 작다면 전자는 Barrier를 느끼지 못하고 insulator작용을 하지 못합니다.
$$if~a<\Delta x$$
$$\Delta x \sim a_{min}=\frac{\hbar}{2\sqrt{2mW_b}}~(if,~\Delta p\geq \sqrt{2mW_b})$$
계산 결과는 위에 표에 나와있습니다.
물론 defect과 같은 외부요소를 고려 안한것이므로 실제론 더 두꺼워야 할 수 있습니다.
하지만 이 Energy Barrier가 시사하는 바는 아무리 insulator라 하더라고 thin film에서는 leakage current가 있을 수 밖에 없습니다.
그렇다면 leakage가 존재할 경우 전하량은 어떻게 될까요?
바로 커패시터와 저항이 병렬로 구성되어있는 회로와 같게 될 것 입니다.
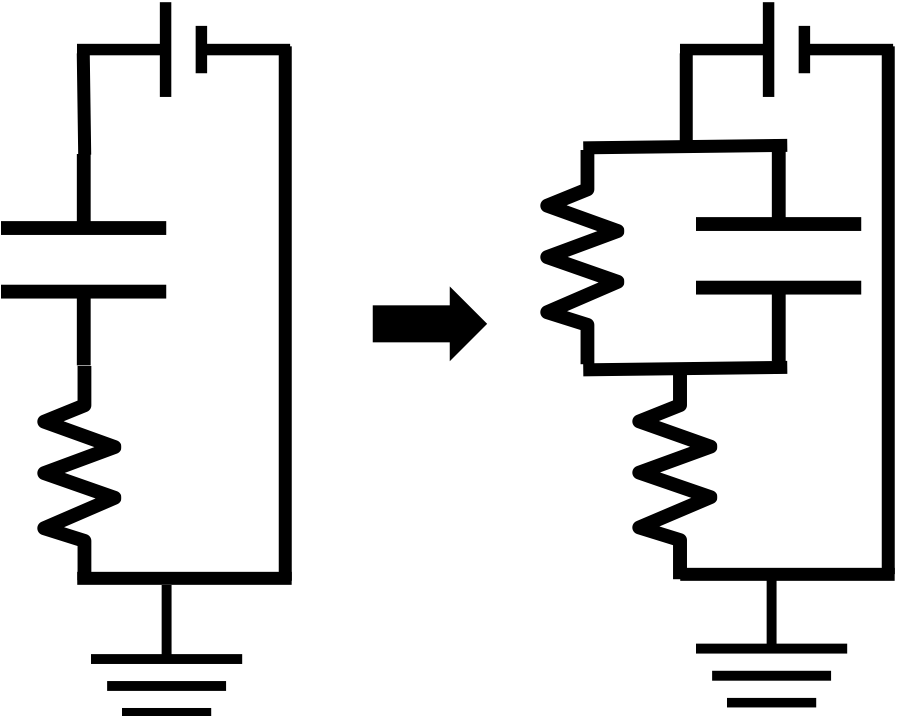
그렇다면 단순히 두 저항에 Voltage Dividing되는 정도로 계산이 되고 커패시터에 병렬로 연결된 저항에 걸리는 전압만큼 Charge가 유도 될것입니다.
'전자공학' 카테고리의 다른 글
| Solder Reflow(솔더 리플로우) SMD (0) | 2019.08.01 |
|---|---|
| ReRAM (Redox Based Resistive Ram) (5) | 2019.06.22 |
| 커패시터(Capacitor) _ Insulator (절연체) (0) | 2019.05.24 |
| Magnetic Circuit(자기 회로) (0) | 2019.04.25 |
| 인덕턴스(Inductance) (0) | 2019.04.25 |


