|
정의상 가정 |
수동소자(Passive element) : 멤리스터(memristor), 저항(resistor), 커패시터(capacitors), 인덕터(inductor) |
|
내용상 가정 |
전압이 불연속적으로 끊어진다면, i(t)의 값은 무한대가 되어야한다. 즉 i(t)가 유한하다고 가정한다면 양단의 전압은 불연속할 수 없다. 따라서 i(t)는 유한하다고 가정해야한다. 에너지 관점에서 순시전력으로 계산되어야 하며 순시전력$$P(t)=V(t)\times C\frac{d V(t)}{dt}$$ 이다. 이는 보존력장으로 운동에너지가 같고 에너지 값이 항상 양수여야한다. |
|
공식 |
$$i=C\frac{dv}{dt}v(t)=\frac{1}{C} \int _{t_0}^{t} i (\tau) d \tau + v(t_0) $$ |
|
단위 |
F |
|
응용 |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
Capacitor는 두 판 사이에 전압이 형성됬을때 충전되는 소자로, 물질의 관점에서는 insulator라 생각하면 되고 전자공학적 입장에서는 고주파에서는 short, DC 및 저주파에서는 open으로 보는 회로적인 모델입니다.
한국어로 축전기라고 하는 이 커패시터는 사실 모양부터 굉장히 많다.
사실 현재 반도체에서 응용되는 3D 전자소자의 경우 이 capacitor의 모양을 변화시켜 발전시켰다고 보면 된다.
그렇다면 모양을 하나씩 보도록 하겠다.
아래 그림은 총 3가지의 모양으로 간단한 순인 평행한 축전기, 원통형 축전기, 구형 축전기를 보겠습니다.

먼저 (a)인 평행한 축전기를 보겠습니다. 모든 축전기는 가우스 법칙으로 해결됩니다.
$$\oint \vec {E} d\vec{A}=EA=\frac{q_0}{\varepsilon_0}=\frac{\sigma A}{\varepsilon _0}$$
$$E=\frac{\sigma}{\varepsilon}$$
여기서 평형상태가 된다면,
$$\Delta V=\frac {\sigma}{\varepsilon}d, Q=\sigma A'$$
$$\sigma =\frac{Q}{A'}\rightarrow \Delta V=\frac{d}{\varepsilon}\frac{d}{A}$$
$$C=\frac{Q}{\Delta V}=\varepsilon _0 \frac{d}{A}$$
로 굉장히 익숙한 커패시터의 원리를 따르게 됩니다.
두번째 원통형의 경우
$$\oint \vec {E} d\vec{A}=E2\pi r l=\frac{q}{\varepsilon_0}=\frac{1}{\varepsilon_0}\lambda l$$
$$E=\frac{\lambda}{2\pi \varepsilon _0 r}$$
$$\Delta V=V_b-V_a=-\int_a^b\vec{E}d\vec{s}=-\int_a^b \frac{\lambda}{2\pi \varepsilon _0 r}dr=-\frac{\lambda}{2\pi\varepsilon}ln\frac{b}{a}$$
$$C=\frac{Q}{|\Delta V|}=\frac{\lambda l}{\frac{\lambda}{2\pi \varepsilon_0}ln\frac{b}{a}}=\frac{2\pi\varepsilon_0 l}{ln\frac{b}{a}}$$
세번째 구의경우까지 보면 대충 어떤식으로 계산하는지 감이 잡힐 겁니다.
$$\oint \vec{E}d\vec{A}=E4\pi r^2=\frac{Q}{\varepsilon_0}$$
$$E=\frac{Q}{4\pi r^2\varepsilon_0}$$
$$\Delta V=-\int_a^b\frac{1}{4\pi \varepsilon_0}\frac{Q}{r^2}dr=\frac{Q}{4\pi\varepsilon_0}(\frac{1}{b}-\frac{1}{a})$$
$$C=\frac{Q}{\Delta V}=4\pi\varepsilon_0\frac{ab}{b-a},(b\rightarrow \infty,4\pi\varepsilon_0 a)$$
대충 가우스 법칙을 때리면 어느정도 걸릴 것입니다.
대충 보았으니 이제 회로에서 작용을 보겠습니다.

이 회로적으로 표현할때는 한가지만 명심하면 됩니다. 바로 도선에서는 즉 금속에서는 전하가 언제나 평행이기 때문에 금속에 있는 전하를 모두 더하면 0이라는 것입니다. 또한 도체 펴면에서는 전압이 같다는 것을 명심하면 됩니다.
먼저 병령(a)의 경우 커패시터를 연결하는 도선에서는 전압이 같아 양단의 전압이 같다는 것입니다.
즉 전하량에서 차이가 나게 되는데,
$$Q_{Tot}=Q_1+Q_2=C_1\Delta V+C_2\Delta V=C_{eq}\Delta V$$로
$$C_{eq}=C_1+C_2$$입니다.
즉 병렬은 단순히 커패시터 하나의 면적이 커지는 효과로 보면 됩니다. 그렇다면 직렬을 어떨까요?
바로 두 커패시터를 이어주는 도선은 어쨋든 중성이므로 각 커패시터로 분리가 되는 두 전하량은 정해져 있습니다.
따라서 두 커패시터에는 같은 전하량이 유도가 됩니다.
즉 두 커패시터에서 가해준 전압을 나눠같는다고 할때
$$\Delta V=\Delta V_1+\Delta V_2=\frac{Q}{C_1}+\frac{Q}{C_2}=\frac{Q}{C_{eq}}$$
로 단순히 거리가 멀어지는 효과로
$$\frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}$$
물론 이들은 안정이 된 상태입니다. 이렇게 안정이 된 상태는 전하를 유도하는 특수한 상황이외에서느 잘 사용하지 않습니다.
즉 DC에서는 open된 상태이므로 고주파에서 잘 사용하는데 이를 이용하는게 바뀌는게 곧 transiant상황입니다.
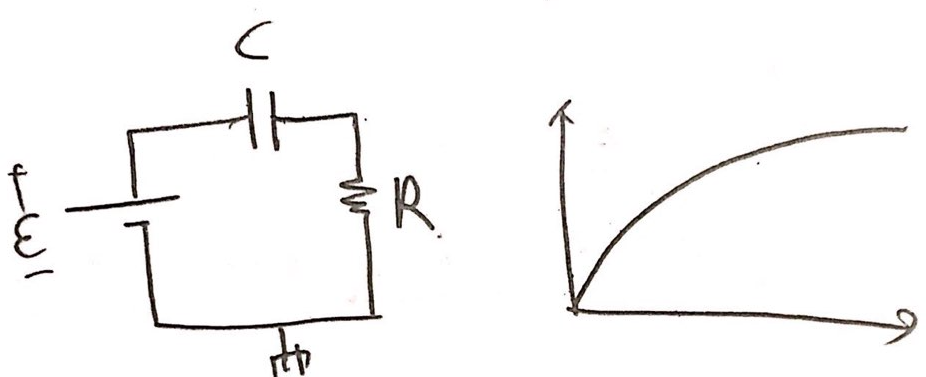
다음과 같은 회로를 가정한다하고 전압을 딱 가해보겠습니다.
$$\varepsilon=\frac{Q}{C}+R\frac{dQ}{dt}$$인 상태로 변화하는데 오랜시간이 지나면 물론 위에서 유도한 식처럼 되는데, 이런상황을 saturation이라 하고
$$\frac{Q_\infty}{C}=\varepsilon$$이라 가정을 한다면
$$Q(t)=Q_\infty+\tilde{Q}$$
$$\varepsilon=\frac{Q_infty}{C}+\frac{\tilde{Q}}{C}+R\frac{d\tilde{Q}}{dt}$$
$$\frac{d\tilde {Q}}{dt}=-\frac{\tilde{Q}}{RC}$$
$$\tilde{Q}(t)=\tilde{Q}(0)e^{-\frac{t}{RC}}$$인데
$$Q(0)=\varepsilon C_+\tilde{Q}(0)=0, ~~\tilde{Q}(0)=-\varepsilon C$$
$$Q(t)=\varepsilon C [1-e^{-\frac{t}{RC}}]$$
다시말해 capacitor가 전하를 유도시키는 시간은 인가되는 전압라인의 저항과 커패시턴스에 비례합니다.
다음은 에너지 관점에서 살펴볼 건데요

다음과 같은 상태에서 커패시터를 대전시키는데 필요한 에너지는
$$\Delta W=\Delta V\cdot dq=\frac{q}{C}dq$$
$$W=\int_0^Q\frac{q}{C}dq=\frac{Q^2}{2C}$$
$$U=\frac{Q^2}{2C}=\frac{1}{2}C(\Delta V)^2\frac{1}{2}\frac{1}{\varepsilon_0}\frac{A}{d}E^2d^2=\frac{E^2}{2\varepsilon_0}frac{Ad}$$입니다. 이때 회로 관점에서는 위의 회로에서
$$V_{Bolt}=\varepsilon\int_0^\infty I(t)dt$$
$$I=\frac{dQ}{dt}=\frac{\varepsilon C}{RC}e^{-\frac{t}{RC}}=\frac{\varepsilon}{R}e^{-\frac{t}{RC}}$$
$$V_{Bolt}=\frac{1}{2}\frac{Q_{\infty}^2}{C}+R\int_0^\infty I^2(t)_dt$$
커패시터 자체로는 시간의 미분으로 정의할 수 있는데,
$$i=C\frac{dv}{dt}$$이며 역으로
$$v(t)=\frac{1}{C}\int_{t_0}^{t}i(\tau)d\tau+v(t_0)$$이다.
지금까지는 충분히 두꺼운 절연체를 가진 커패시터를 논했는데요.
다음포스팅 Thin Film Insulator_Capacitor(박막 커패시터)에서는 얇은 박막의 커패시턴스를 보겠습니다.
'전자공학' 카테고리의 다른 글
| ReRAM (Redox Based Resistive Ram) (5) | 2019.06.22 |
|---|---|
| Thin Film Insulator_Capacitor(박막 커패시터) (2) | 2019.05.25 |
| Magnetic Circuit(자기 회로) (0) | 2019.04.25 |
| 인덕턴스(Inductance) (0) | 2019.04.25 |
| 동축케이블(coaxial cable) (1) | 2019.02.12 |


