|
정의상 가정 |
Nearly free electron model_밴드갭(band gap) |
|
내용상 가정 |
각 초전도체의전하의 갯수는 초전도체면 거의 같다고 가정할 수 있다. |
|
공식 |
$$kT_c\sim \hbar \omega _D e^{-1/\lambda}$$ |
|
단위 |
|
|
응용 |
|
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
초전도체는 말그대로 저항이 0인 물질입니다. 아쉽게도 저항이 0이되려면 굉장히 낮은 온도라는 조건이 붙게되는데,
많은 연구자들이, 이들이 상온에서 동작시키기 위해 열심히 동작 온도를 높이다가 현재는 거의 포기한 상태입니다.
높은 온도와 낮은온도의 기준은 30K이며, 이 초전도성을 잃게 되는 온도를 지금부터 Tc라 하겠습니다.
Low Tc로는 Metal이나, Alloy가 있고, High Tc로는 Oxide나 CuO2, Iron based, Metalic Hydrogen와 같은 물질이 있습니다.
T>Tc인 상태를 비저항이 0이 아닌 normal state라 하고, T<Tc인 비저항이 0인 상태를 Meissner Effect상태라 하고 magnetic susceptibility가 $$\chi <0$$으로 외부 자기장과 반대방향으로 자기장이 생겨 완전히 상쇄시키는 특징을 가집니다.(저항이 0이라 Diamagnet입장에서 외부에 자기장이 들어올때 와전류를 무한정 생성해 낼 수 있습니다) 아래 가장 왼쪽 그래프와 같은 개형입니다.

중간그래프는 자기장을 세게 가해주면 Tc가 점점 0으로 떨어집니다. 이를 임계 자기장이라 하며 Hc라 합니다. 또한 임계전류 밀도보다 낮아진다면, 초전도가 깨지는 현상이 발생합니다.
지금까지는 단순한 초전도체에 대한 성질을 보았는데요,
이제 이들이 왜 이렇게 나오는지 설명하는 여로 이론들을 살펴보겠습니다.
그 중 가장 깊게 받아들여지는 이론이 바로 BCS모델입니다.
이는 Cooper pairs즉 전자들이 단독으로 움직이지 않고 두개가 한번에 움직인다는 이론입니다.
단순이 임의이 전자 두개가 묶여있는것이 아닌, momentum과 spin이 모두 반대인 전자들이 묶여있는 것입니다. 다시말해 $$|\vec k \uparrow , -\vec k \downarrow|$$입니다. 이들은 이동하는 경향을 다음 그림과 함께 살펴보겠습니다.
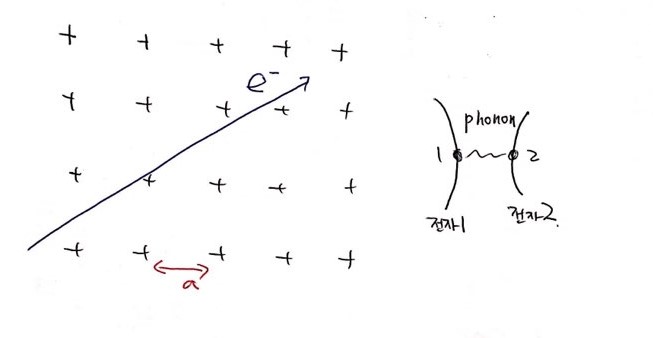
다음과 같은 격자에 전자가 쭉 휘졌고 다니면, 상호작용으로 영향을 주게 됩니다. 이 상호작용을 electron phonon interaction이라고 하는데요, 즉 원자가 휘졋고다니는 전자에 의해 떨게 되는데 이 떠는 frequency를 Debye frequency라 하고 이를 phonon이라 합니다. 다시 본론으로 돌아와서 이 전자는 fermi surface 주변에서 자유롭게 돌아다니기 때문에
$$\vec k \sim |k_F|\hat k,~~~~k_F \sim \frac{mv_F}{\hbar}$$
인데, 원자와 원자 사이 a를 지나가는 데 걸리는 시간은
$$T_e=\frac{a}{v_F}\approx\frac{3\times 10^{-10}m}{10^6 m/s}\sim 3\times 10^{-16}sec$$이며, lattice vibration 관점에서는 Ddbye frequency가 주요하므로,
$$T_l\sim \frac{1}{\omega_D}=10^{-13}sec$$
$$\frac{T_l}{T_e}\sim 3000$$
입니다. 따라서 먼저 통과하는 전자 1은 흔적을 남기며, 뒤이어 오는 전자 2가 이 흔적을 때문에 느끼는 상호작용이 다릅니다. 따라서 두 전자가 격자를 매개로 상호작용을 하게 되는 것이고, 이를 cooper pair라 합니다.(더 직관적인 설명으로는 전자가 lattice를 끌어당겨 + potential을 발생시켜 주변 전자들이 거기에 모여 같이 다니게 된다는 설명도 있습니다.)
다시말해 두 전자사이에 속박 energy가 발생하는데, 열 에너지로 끊기게 됩니다. 따라서 상온에서는 결코 유지되지 않습니다. 이 속박 에너지가 크면 클수록 Tc가 커집니다.
갑자기 이 Cooper pairs의 개념을 꺼낸 이유는 전자 두개가 뭉쳐서 한개처럼 다니면 신기한 현상이 발생하기 때문입니다. 입자에는 크게 Fermion과 Boson이 있는데, 우리가 익히 알고있는 파울리 베타원리나 다른 상호작용의 영향을 받는것은 바로 Fermion입니다. 하지만, 전자 두개가 하나로 다녀 이런 영향을 받을 수 있는 spin이나 momentum과 같은 것을 다 상쇄시켜 버린다면 Boson처럼 다닐 수 있고 따라서 외부에 lattice와의 상호작용을 받지 않아 어떠한 저항도 받지 않습니다.
이 상호작용은 electron-phonon interaction이고 이는 electron bound pairs이고 이로 인해 binding energy가 생기고, 따라서 binding에너지가 생기면 언제나 발생하는 energy gap이 생기게 됩니다.

즉 위 그림과 같이 Fermi level 사이에 Energy Gap가 생기게 되고 전후로 Bosonic ground state, Fermionic state라 합니다.이는
$$E_g=2\Delta e$$
입니다. 이 Energy Gap의 의미는 무엇일까요?? 이것은 Band Gap이랑은 전혀 다른 개념입니다. Band Gap이 단순히 전자가 자유전자가 되기 위한 Gap이라고 한다면 여기서의 Energy Gap은 Cooper pair가 유지되는 gap입니다. 다시말해 열이나 여타 다른 에너지 때문에 이 Energy Gap을 넘어가게 된다면, normal한 electron phonon scattering이 발생하게 되어 Normal한 electron이 되게 됩니다.
(더 정확하게는 Semiconductor의 Band gap은 lattice의 phonon이 Gap을 주고 여기서는 electron-electron으로 발생하는 Gap입닏. 즉 전자와 전자의 상호작용으로 매개하는것이 phonon일 뿐입니다.)
따라서 Energy gap은 Tc가 넘어가면 그냥 넘어가게 되고 이 Tc를 환산한다면
$$kT_c\sim \hbar \omega _D e^{-1/\lambda}$$
가 되게 됩니다. 식에서 w를 볼떄 w는
$$\omega _D \sim \frac{1}{M^\alpha}, ~~ \alpha \sim \frac{1}{2},~~\lambda =D(E_F)V$$ 의 관계를 가져 무거우면 무거울수록 낮아지므로 Tc가 낮아집니다. 또한 V는 electron phonon interaction potential입니다. 즉
$$\Delta (T) \approx 3.2 k T_C(1-\frac{T}{T_C})^{1/2}$$의 관계로 Tc를 완전히 넘지 않을 때 까지는 회로적인 병렬 효과로 여전히 저항은 0이게 됩니다.
Gap을 넘어 Excitation이 되면 어떨까요? 그냥 quasi particle이 되고 pair가 broken됩니다.
이외 Two-fluid model로 액체 헬륨의 viscosity가 0인 super fluid라는 것과 Normal 전자와 superconducting electron이 공존하는 상태도 있습니다.
$$n_s=n[1-(\frac {T}{T_c})^4]$$
이제 초전도체의 핵심 특성이라 할 수 있는 자기장과의 관계를 보겠습니다.
바로 Meissner Effect인데요. 두가지 type을 나눠서 고려해볼 수 있습니다. 자기장을 완벽하게 막는것과 어느정도는 투과하는 타입 두개로 나눠 보겠습니다.
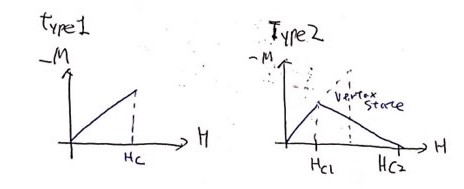
먼저 Type1의 경우 내부자기장이 항상 0인 B=0인 상태입니다.
$$B=H+4\pi M=0$$
$$M=-\frac{H}{4\pi}$$
$$\chi=\frac{M}{H}=-\frac{1}{4\pi}$$ 입니다. 반면 type 2는 어느정도 외부자기장이 침투하여 다발형태로 침투하는 즉 아래 그림과 빨간색과 같은 형태로 Magnetic Flux가 형성됩니다. 이때 type2의 Hc1에서 Hc2까지의 영역을 vertex state라 합니다.

이외 Heat capacity은 위 그래프처럼 나타날 수 있습니다.
이제 London equation을 기본으로 앞서 보여드렸던 성질들을 살펴보겠습니다.
기본적으로 전자의 갯수를 본다면 superconductivity의 정의자체에의해
$$T=0\rightarrow ~~n_s=n$$
$$T=T_C\rightarrow ~~n_s=0$$
$$\frac{n_S}{n}=\frac{\Delta ^2(T)}{\Delta_0^2}$$의 성질이 있습니다.
이제 2-fluid model을 사용하여 위 성질에 대해 논의해보겠습니다.
기본적인 model식은
$$\psi = A(\vec r )e^{i\phi(\vec r )}$$
$$\psi \psi ^* =A^2=n_s$$
따라서
$$\psi = n_s^{1/2}e^{i\phi}$$
입니다. 여기서 전자가 pair로 다니므로 정의가 다음과 같이 바뀝니다.
$$n_s \rightarrow 2n_s,~~q\rightarrow 2e$$
입니다. 또한 운동량 또한 자기장을 고려하여 고쳐쓸 수 있는데
$$\vec P= m \vec \nu =-i\hbar \vec \nabla -\frac{q}{c}\vec A$$
이를 이용하여 전류를 유도할수 있는데 단순 대입이니 주의깊게 보지 않아도 됩니다.
$$\vec J =n_s q \vec v _s=q\psi* \vec \nu \psi=(-2e)\frac{n_s}{m}e^{-i\phi(\vec r )}[-i\hbar \vec \nabla +\frac{2e}{c}\vec A]e^{i\phi}$$
$$=-2e\frac{n_s}{m}[-i\hbar (i\vec \nabla \phi) +\frac{2e}{c}\vec A]$$
이제 자기장을 도입할 수 있습니다. 다음과같은 기본원리를 이용해서(여기서 j는 전류입니다.)
$$\vec \nabla \times \vec \nabla \phi =0,~~~\vec \nabla \times \vec A =\vec B,~~\vec \nabla \cdot \vec A =0$$
$$\vec \nabla \times \vec j =-(2e)^2(\frac{n_s}{m_c})\vec B$$ 다시 다음식에 대입할 수가 있는데
$$\vec \nabla \times \vec B =\frac{4\pi}{c}\vec r$$
$$\vec \nabla \times (\vec \nabla \times \vec B)=\frac{4\pi}{c}\nabla \times \vec j_s$$
$$-\nabla^2B=-[\frac{4\pi}{c}(2e)^2\frac{n_s}{m_c}]$$
이제 여기서 superconductor일때 외부자기장이 가해졌을떄 얼마나 침투하는지 침투하는거리를 구해보겠습니다.
$$\nabla ^2\vec B=\frac{\vec B}{\lambda_c^2}$$
로 Cooper pair로 바꾼다면
$$\lambda_c^2=\frac{2(m_e)c^2}{4\pi(2e)^2n_s},~~\lambda_c \approx 100\sim 300nm$$
입니다. 이를 London penetration depth라 하고 정말 pure한 superconductor는 50nm투과하고 사라집니다. 다시말해 아래 그래프 처럼 보이는 것입니다.

따라서 superconductor 내부의 자기장으로만 생각해본다면
$$\nabla ^2 B=\frac{d^2B}{dz^2}=\frac{1}{\lambda_c^2}B\rightarrow ~B=B_0e^{-z/\lambda_c}$$
입니다. 이때 이 depth를 넘어가면 내부 자기장은 바로 0이 되게 되는데 그렇다면 아래식과 같이 유도 전류도 0이되고 유도전계도 0이 되게 됩니다.
$$\vec \nabla \times \vec B =\frac{4\pi }{c}\vec j ; ~B=0\rightarrow ~ j=0$$
$$j_s=0 ~(inside)~\vec j=\rho E=0 \rightarrow ~\vec \varepsilon =0$$
투과하는 자기장이 이렇다고 치면, superconductor의 전자밀도는 어떻게 변화할까요? 이 전자 pair의 형태가 superconductor의 핵심이기 때문에 고려하는것은 무척 중요합니다. 자기장을 생각하지 않고 normal metal에서 super conductor로 변화할 때까지의 길이를 생각해볼때 이 길이를 intrinsic coherence length라 합니다. 예상과 드르게 앞선 London penetration depth와 독립적입니다.
이들은 슈뢰딩거 방정식으로 거리에 따른 전자밀도의 거등을 알아보면 됩니다.
$$-(\frac{\hbar^2}{2m}\nabla^2+V)\psi=E\psi$$
이때 본 상황에 맞는 여러가지 기호의 정의와 가정을 할 수 있는데 바로
$$Energy gap parameter:\Delta,~E=E_F-\Delta,~~\Delta <<c<<E_F,~~k_F\rightarrow~k_F-q_0,~~q_0<<k_F$$
입니다. 이것을 슈뢰딩거 방정식에 대입하여
$$\frac{\hbar^2}{2m}(k^2_F-2k_Fq_0+q_0^2)=E_F-\Delta$$
$$\frac{\hbar^2}{2m}(2k_Fq_0)=\Delta$$
$$\frac{1}{q_0}=\frac{\hbar^2k_F^2}{m\Delta}=\frac{\hbar V_F}{\Delta}=\xi_0$$
입니다. wave vector가 변화할때 이 길이는 증가하며 , energy gap이 클수록 줄어듭니다.
또한 전자밀도는 energy gap과 비례하는데,
$$\sqrt{\Delta}\sim\sqrt{n_s}$$ 의 관계를 가집니다.
cohoerence length가 짧을수록 초전도체가 경계의 영향을 더 많이 받고 여러 외부요소에 더 민감하게 됩니다.
위 London penetration depth와 이 cohoerence length의 비는 초전도체가 자기장에 영향에서 얼마나 벗어날 수 있는지의 척도 K가 될 수 있습니다.
$$K=\frac{\lambda}{\xi},~~K<\frac{1}{\sqrt 2} : type 1,~K>\frac{1}{\sqrt 2} : type 2$$

다시말해 위 그래프에서도 보이듯 자기장에의해 $$\lambda<<\xi$$이라면 type1으로 자기장에 영향을 받지않는 초전도체가 되며 이때 경계의 에너지는 양수가 됩니다., 이 반대이면 type2로 자기장이 어느정도 침투하는 상태입니다. 이떄 interface energy는 음수가 됩니다. 여기서 N은 normal metal이고 s는 superconductor입니다. 추가로 자기장이 통과할때 토오가하는 자기장이 연속적이지 못한데, 이는 초전도체 전자의 wave function
$$\psi=n_s^{1/2}e^{i\phi(\vec r)}$$에서 전류를 고려한다면
$$\vec j_s=-(2e)\frac{n_s}{2m^*}[\hbar \nabla \phi-\frac{2e}{c}\vec A]$$
이고 내부에서 전류는 0이므로
$$\nabla \phi (\vec r)=\frac{2e}{\hbar c}\vec A$$
$$\oint _s\vec \nabla\phi \cdot d\vec l =\phi_1-\phi_2=\Delta \phi=2\pi n$$
으로 flux가 양자화 되는 것을 알 수 있습니다. 위 식을 윗위 식에 대입한다면
$$2\pi n =\frac{2e}{\hbar c}\oint \vec A\cdot d\vec l=\frac{2e}{\hbar c}\int\vec \nabla\times \vec A\cdot d\vec s=\frac{2e}{\hbar c}\int_s \vec B\cdot d\vec l$$
따라서 자기장을 flux로 나타낸다면,
$$2\pi n=\frac{2e}{h c}\Phi\rightarrow~~\Phi=(\frac{h c}{2e})n$$으로 기본 값(2E-11 T/cm2)의 정수배가 됩니다. 이 원리는 SQUID라는 측정장비에서 사용됩니다.
마지막으로 아래와 같은 superconductor사이에 insulator가 있는 상황의 tunneling를 보겠습니다.

이들을 Josepson Tunneling이라 하는데, 기존의 tunneling 식인
$$\psi\psi^*\sim exp[-\frac{2}{\hbar}d\sqrt {2m(V_0-E)}]$$
에서 초전도체는 pair로 다니므로, barrier는 두배로 해서 계산해야합니다. 먼저
$$T=<\psi_1|H|\psi_2>$$라 정의한다면 각각의 영역 S1, S2는
$$S_1:~i\hbar\frac{\partial \psi_1}{\partial t}=\hbar T \psi_2$$
$$S_2:~i\hbar\frac{\partial \psi_2}{\partial t}=\hbar T \psi_1-2eV\psi_2$$입니다. S2의 경우 potential barrier항이 추가됩니다. 여기에 다음과 같은 가정을 추가하여 여러 식을 정리한다면,(전하의 갯수는 초전도체면 거의 같다고 가정할 수 있다.)
$$\psi=\sqrt {n_s}e^{i\phi},~~n_{s1}\approx n_{s2}\approx n_s$$
$$\frac{i}{2}\frac{\partial n_{s1}}{\partial t}-n_s\frac{\partial \phi_1}{\partial t}=n_s T e^{i(\phi_2-\phi_1)}$$
$$\frac{i}{2}\frac{\partial n_{s2}}{\partial t}-n_s\frac{\partial \phi_2}{\partial t}=n_s T e^{i(\phi_1-\phi_2)}-\frac{2eV_{ns}}{\hbar}$$
위 두 식을 real part와 imaginary part로 나뉘어 계산한다면,
real part의 경우
$$\phi_1-\phi_2=\frac{2eV}{\hbar}t+\delta$$
imaginary part의 경우
$$\frac{\partial n_{s1}}{\partial t}=-\frac{\partial {n_{s2}}}{\partial t}=n_sTsin(\phi_2-\phi_1)$$
입니다. 이는 전류관점으로 볼때
$$j\sim \frac{\partial n_s}{\partial t}$$
$$j=j_c sin (\phi_2-\phi_1)=j_c sin(\frac{2eV}{\hbar}t+\delta)$$
으로 밀도의 변화가 전류와 비례하며 V=0이면 DC Josephson effect를 받고 V가 0이 아니라면 AC Josephson effect라 하여 위 오른쪽그림처럼 거동을 하게 됩니다.
참고로 이해가 잘 안되셨다면
https://www.youtube.com/watch?v=fuloQcljFOs 에서 정말 쉽고 짧게 잘 설명되어있습니다.
'물리학' 카테고리의 다른 글
| Polariton (0) | 2019.06.09 |
|---|---|
| Ferroelectricity (강유전체) (2) | 2019.05.27 |
| Energy Band(에너지 밴드)_Tight Binding Model (1) | 2019.05.20 |
| Effective Mass(유효질량) (0) | 2019.05.14 |
| 토크(torque) (1) | 2019.04.25 |

