| 정의상 가정 | 격자(lattice) 분극 _ 이온분극, 배향분극 ( 쌍극자분극 ), 계면분극 Dielectric (유전체) _ plasmon Polariton |
| 내용상 가정 | |
| 공식 | |
| 단위 | |
| 응용 |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
강유전체, 즉 Ferroelecticity는 외부 전계없이도 영원히 분극되어있는 물질입니다.
다시말해 전계 source라도 봐도 괜찮겠네요.
이는 전적으로 물질의 결정구조에 의해 나타납니다.
즉 축이 한개밖에 없는 재료일떄 한방향으로만 분극 현상이 발생할 수 있습니다.
다시말해 point group 32개에서 중간점 대칭인 12개를 빼면 20개가 남는데, 이들을 압전성 구조라 하고 이중 자발 분극이 생기는 10개의 결정구조를 강유전성, 초전도성 결정구조라 합니다. 예를 들어 BaTiO3의 경우 130도 이상에서는 입방단위셀을 가지므로 Ti가 단위결정의 중심질량에 위치하지만, 130도 이하로 내려간다면, 사방정계가 되어 Ti원자가 질량중심에서 떨어져서 위치하게 되어 양전하와 음전하가 분극을 이루게 됩니다. 이떄 130도를 Curie 온도라 하며, 아 아래의 온도로 떨어지면 결정구조가 외곡되어 자발적 분극이 생기게 됩니다.
왜그럴까요? 이는 단순히 결정에너지 덕분에 발생합니다. 즉 각 단위 셀 내부의 Ti원자가 이동해 결정의 변위가 늘어나면 결정에너지는 낮아집니다. 또한 이런 단위 결정들이 모여 쌍극자가 모두 한방향으로 정렬 되면 쌍극자 상호간의 에너지때문에 전체 결정의 에너지 준위가 낮아집니다.
단 이는 공정상에서 결정이 되는데, Curie Temperature 이상에서 전걔를 가하며 온도를 내린다면 전걔방향으로 자발분극 P를 유도할 수 있습니다. 이를 poling이라 하며, 이때 공식은
입니다. 따라서 전류로 나타내면 $$I=A\frac{dP}{dt}$$로 나타낼수 있습니다. 이때 A는 면적입니다.
이제 광학적인 현상을 살펴볼 건데, 이는 Polariton에서 논의한 사항을 가져와 쓰겠습니다.
강유전체에 가장큰 특징은 바로 local field가 있다는 것입니다. 이 local field는 격자의 transverse normal mode의 주파수 $$\omega_{TO}$$를 줄어들게 합니다. 또한 낮은 온도에서는 thermal fluctuation이 작아지므로 또한 주파수를 작게 합니다. 이를 soft phonon이라 하고 다음과 같이 식이 쓰입니다.(이는 Dielectric (유전체) _ plasmon후반부에서 정리하였습니다.)
$$\epsilon (0)=\epsilon _\infty \frac{\Omega^2_p}{\omega^2_{TO}},~~\Omega_p=\frac{4\pi(Ze)^2n}{\mu}$$
온도에 따라서는
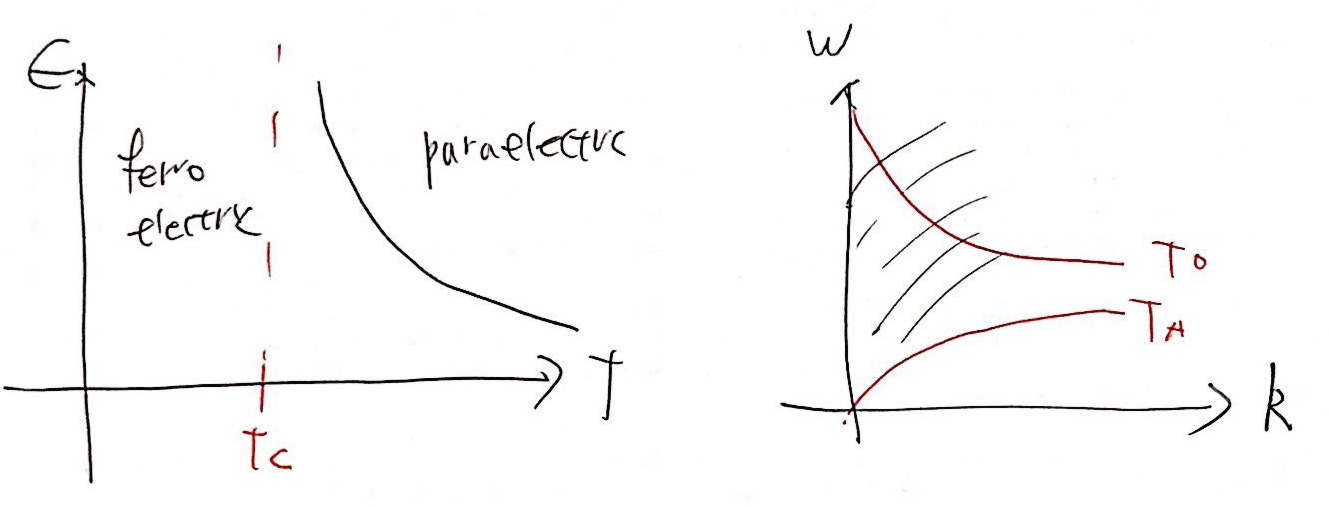
다음과 같은 경향을 보이고 보통 $$\omega^2_{TO}\propto T-T_C,~\epsilon^{-1}(0)\propto T-T_C$$인 경향도 보입니다.

local field의 강한 힘에서 물질은 Tc근처의 일반적인 position에 머무르고 있다가 새로운 equilibrium 지점에 도착하면 이온을 옮깁니다. 이렇게 이온이 이동하여 permanent polarization P를 갖게 됩니다. (물론 T<Tc에서만 일어납니다.)
'물리학' 카테고리의 다른 글
| 강유전체 측정 ( Ferroelectric measurement ) (2) | 2020.01.17 |
|---|---|
| Polariton (0) | 2019.06.09 |
| 초전도체 (superconductivity)_BCS model, Cooper pair, Josephson tunneling (0) | 2019.05.20 |
| Energy Band(에너지 밴드)_Tight Binding Model (1) | 2019.05.20 |
| Effective Mass(유효질량) (0) | 2019.05.14 |



