|
정의상 가정 |
|
|
내용상 가정 |
|
|
공식 |
$$\epsilon =\epsilon _\infty+\frac{\Omega_p^2}{\omega_{To}^2-\omega^2},~~\Omega^2_p=\epsilon _\infty (\omega_{Lo}^2-\omega^2_{To})$$ |
|
단위 |
|
|
응용 |
|
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
polariton이라는 개념은 phonon과 photon을 합친 개념입니다.
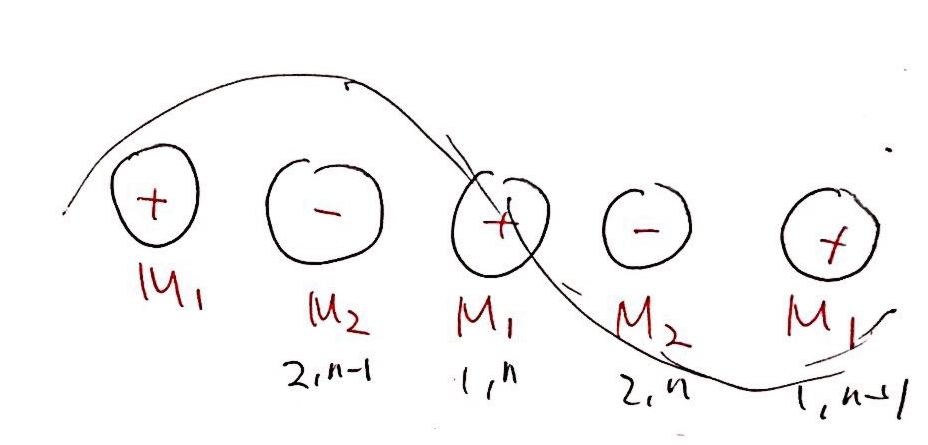
먼저 위의 그림은 빛의 방향 K와 전기장의 방향이 수직인 TO phonon mode를 나타낸 그림입니다. 수직하기 때문에 다음이 성립합니다.
$$\vec K \cdot \vec E=\vec \nabla \cdot \vec E =0$$
원자와 전자가 겹쳐있는것을 나타낸 것입니다. 각 wave의 위치를 u라고 한다면 간단한 운동방정식을 세울 수 가 있는데,
$$-M_1\omega ^2 u_{1,n}=-K(u_{1,n}-u_{2,n})-K(u_{1,n}-u_{2,n-1})+q_1\vec E$$
$$-M_2\omega ^2 u_{2,n}=-K(u_{2,n}-u_{1,n+1})-K(u_{2,n}-u_{1,n})+q_2\vec E$$
여기서 장파장 모드만 중요하다고 한다면 다음의 근사가 가능합니다.
$$u_{1,n}=u_{1,n\pm 1}=u_+,~~u_{2,n}=u_{2,n\pm 1}=u_-,~~q_1=Ze,~q_2=-Ze$$
윗식을 윗윗식에 대입하고 M을 나누고 더한다면
$$-\omega^2(u_+ -u_-)=-(\frac{2K}{M_1}+\frac{2K}{M_2})(u_+-u_-)+(\frac{Ze}{M_1}+\frac{Ze}{M_2})E$$
여기서 E=0임을 가정하고 다음식에서 𝞵를 정의한다면
$$\omega^2=2K(\frac{1}{M_1}+\frac{1}{M_2})=2K\frac{1}{\mu}\rightarrow \omega_{To}=\sqrt{\frac{2K}{\mu}}$$
으로 대입한다면
$$(\omega^2_{To}-\omega^2)(u_+-u_-)=\frac{Ze}{\mu}E$$
$$\Delta u=\frac{Ze/\mu}{\omega^2_{To}-\omega^2}E$$
이고 Polarization의 정의에 의해서
$$P=nZe(u_+-u_-),~~D=E+4\pi P =E+4\pi n Ze(\Delta u)=\epsilon E$$
에대가 앞서 구한 u를 대입 할 수 있습니다.
$$\epsilon E =E+4\pi n Z e \frac{Ze/\mu}{\omega^2_{To}-\omega^2}E$$
$$\epsilon = 1+\frac{4\pi n (Ze)^2/\mu}{\omega^2_{To}-\omega^2}$$으로 다음과 같은 그래프가 유도되게 됩니다.
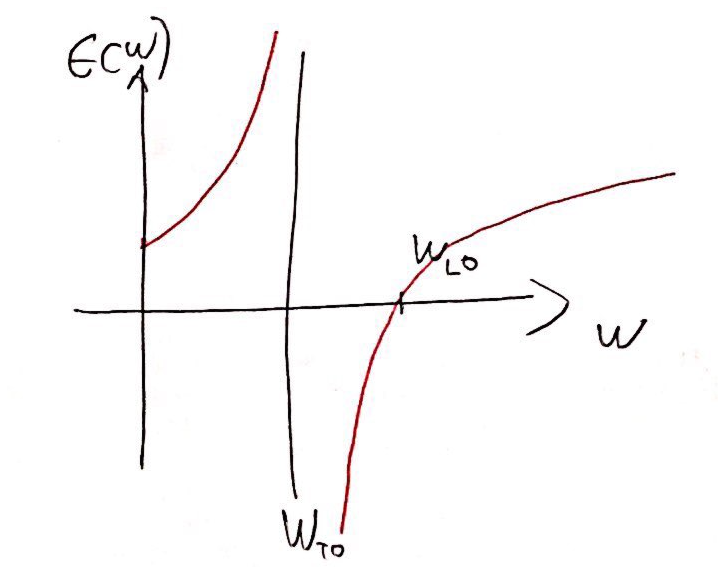
여기에 life time을 포함시키고 high frequency에 대한 𝟄을 𝞮∞라 한다면
$$\epsilon =\epsilon _\infty +\frac{\Omega_p^2}{\omega^2_{To}-\omega^2-i\omega/\tau}, ~~\Omega_p^2=4\pi n \frac{(Ze)^2}{\mu}$$
위와 같은 전개식으로
$$\epsilon(0)=\epsilon _\infty +\Omega^2_p/\omega^2_{To}$$
$$0=\epsilon_{\infty}+\frac{\Omega_p^2}{\omega^2_{To}-\omega^2_{Lo}}$$
$$0=\epsilon_\infty\omega^2_{To}-\epsilon_\infty\omega^2_{Lo}+\Omega^2_p$$
$$\omega^2_{Lo}=\omega^2_{To}+\frac{\Omega_p^2}{\epsilon _\infty}=\omega^2_{To}+\frac{\omega^2_{To}}{\epsilon_\infty}(\epsilon (0)-\epsilon_{\infty})$$
그렇다면 LO mode (K와 전기장 평행)는 어떠할까요??
$$\vec K \cdot \vec E=|\vec K||\vec E|=\nabla \cdot \vec E$$
을 성립하기 때문에 단순 식을 전개해본다면
$$\epsilon =\epsilon _\infty+\frac{\Omega_p^2}{\omega_{To}^2-\omega^2},~~\Omega^2_p=\epsilon _\infty (\omega_{Lo}^2-\omega^2_{To})$$
$$\epsilon =\epsilon _\infty(1+\frac{\omega_{Lo}^2-\omega^2_{To}}{\omega^2_{To}-\omega^2})$$
$$=\epsilon_\infty\frac{\omega^2_{Lo}-\omega^2}{\omega^2_{To}-\omega^2}$$
으로 high frequency에서의 dielectric을 알고 있다면 dielectric 을 알 수 있습니다.
$$\epsilon (0)=\epsilon _\infty\frac{\omega^2_{Lo}}{\omega^2_{To}}$$
이를 LST(Lyddane-Sachs-Teller) Relation이라고 합니다.

또한 Dispersion relation 이라 하여
$$\omega =\frac{CK}{\epsilon}$$
으로 정확하게 서술하면
$$\omega^2=[\epsilon_\infty +\frac{\epsilon (0)-\epsilon (\infty)}{1-\omega^2/\omega^2_{To}}]=C^2K^2$$
입니다.
'물리학' 카테고리의 다른 글
| 음의 전기용량 (negative capacitance) (8) | 2021.05.17 |
|---|---|
| 강유전체 측정 ( Ferroelectric measurement ) (2) | 2020.01.17 |
| Ferroelectricity (강유전체) (2) | 2019.05.27 |
| 초전도체 (superconductivity)_BCS model, Cooper pair, Josephson tunneling (0) | 2019.05.20 |
| Energy Band(에너지 밴드)_Tight Binding Model (1) | 2019.05.20 |



