↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어가실 수 있습니다!!
커패시터(Capacitor) _ Insulator (절연체)는 Q=CV라는 자명한 법칙을 가지고 있습니다. 절연체에 전압을 인가하면 절연체 계면에 Q만큼의 전하가 유도된다는 의미입니다. 여기서 C는 전압 V에 따라 얼마나 Q가 얼마나 유도되는지를 수치화한 상수인데 이를 전기용량 capacitance라 합니다.

상식적으로 +전압에는 전자가 당겨지므로 C는 항상 양수(+)라고 알려져 있습니다.
하지만 AC로 가면 바뀝니다. 다시말해 건전지를 + - + - 반복하다 보면, 어느 순간에는 음수(-)인 C생기게 됩니다.
이와 비슷한 경향은 고체 초고주파 신호 발생기 , 오실레이터 (GHz THz Signal Generation , oscillator)에서도 나오는데, 오실레이터도 회로에 AC로 가할 때 저항이 음 저항(negative resistor)으로 발생함에 따라 형성되는 소자입니다.
물론 일반적인 절연체에 AC를 가한다고 모두 Negative capacitance가 나오는건 아닙니다. 이 절연체는 강유전체이어야 합니다. 본 포스팅에서는 강유전체에서 어떻게 negative capacitance를 형성하고, 이 negative capacitance를 어느 분야에 적용할 수 있는지 살펴보겠습니다.
Negative capacitance를 완벽하게 이해하게 위해서는 강유전체, 분극(Polarization), Net electric field, Free energy, Landau equation이라는 개념을 이해해야 합니다.

먼저 분극은 어떤 물질이 전기장에 의해 얼마나 dipole이 정렬되는가 나타내는 수치입니다. 즉 유전물질에 전기장을 인가하게 되면 분극이 생기게 됩니다. 이렇게 분극이 형성되게 되면, 분극도 +와 -극이 있으므로 분극에 의한 전기장이 추가적으로 생기게 되고 이를 depolarizated electric field이라 합니다. 여기서 외부 전기장에 depolarizated electric field를 뺀 값을 net electric field 합니다.
즉 물질에 실제 걸리는 전기장은 Enet인 net electric field입니다. 분극(polarization)은 모든 유전물질이 갖고 있지만, 강유전체는 특별하게 spontanous polarization을 갖고 있습니다. 이는 외부 전기장이 없어져도 남아있는 분극입니다.
이 분극에 대한 열역학적 free energy (익히 알고 있는 Gibbs free energy의 free energy)에서 이차 상변이를 고려한다면 분극 에너지는 Tayler 이사함수로 근사할 수 있습니다.$$U=\alpha P^2 + \beta P^4 +\gamma P^6 -EP$$로 U가 free energy이고 P는 분극 나머지는 상수입니다. 이 free energy는 분극(전하량)에 대하여 다음과 같은 경향을 띄게 됩니다.
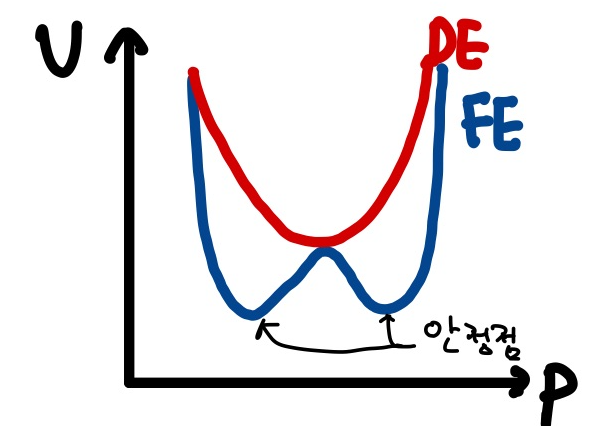
단순 유전체(DE)일 경우에는 0에서 energy가 가장 낮고, 강유전체(FE)에서는 2개의 안정점이 있습니다. 즉 강유전제는 alpha가 음수이고 beta가 양수입니다. 이 2개의 안정점이 바로 spontanous polarization이 유지되는 부근입니다. 이 안정화되는 에너지는 커패시터 구조에서도 polarization이 어떤 상태를 유지할 것인지를 나타내는 에너지로써 에너지 경향은 커패시터 에너지로도 생각할 수 있습니다. 따라서
$$U=\frac{Q^2}{2C}$$이고 이를 본래 커패시터 식인
$$Q=CV \rightarrow C=\frac{dQ}{dV}$$에 대입한다면
$$C=(\frac{d^2 U}{dQ^2})^{-1}$$이 됩니다. 이렇게 에너지와 커페시터의 관계를 살펴보았으니, 만약 negative capacitance가 발생한다면 나타날 경향을 알아보겠습니다.

먼저 positive일 경우 익히 아는 대로, V가 증가할수록 당연히 Q가 증가하고 Q와 U는 이차 함수 모양을 갖습니다. 하지만, negative가 되는 순간, V가 증가할 수록 Q는 감소하며, Q는 U가 음수의 이 차 항이 됩니다.

따라서 U를 볼 때 $$U_{DE}=\frac{(PA)^2}{2C}$$$$U_{FE}=\frac{1}{2}\alpha t_{FE}AP^2+\frac{1}{4}\beta t_{FE}AP^4+\frac{1}{6}\gamma t_{FE}AP^6$$으로 형성이 되어 FE에서 음수의 이 차 항이 해당하는 부분에 negative capacitance가 나온다고 볼 수 있습니다. 이를 capacitor potential (V)로 다음과 같이 변환한다면$$V=\frac{1}{A}\frac{\partial U}{\partial P}$$로 DE와 FE각각$$V_{DE}=\frac{PA}{C}$$$$V_{FE}=\alpha t_{FE}P+\beta t_{FE}P^3+\gamma t_{FE}P^5$$로 그래프가 Q에 따라 감소하는 부근에서 negative capacitance가 나온다고 유추할 수 있습니다. 더 직접적으로 확인하기 위해 C를 다음식으로 구한다면 $$C=(\frac{1}{A}\frac{\partial V}{\partial P})^{-1}$$$$C_{DE}=constant$$$$C_{FE}=\frac{A}{\alpha t_{FE}+3\beta t_{FE}P^2+5\gamma t_{FE}P^4}$$로 직접적인 negative capacitance를 확인할 수 있습니다.
그렇다면 왜 negative capacitance가 나올까요?
만약 전기장이 가해져있는 어떤 강유전체 물질에 반대 방향으로 빠르게 전기장을 가해보겠습니다.

시간에 따라 반대 방향 외부 전기장이 커질 텐데, 강유전체의 spontanous polarization은 어떻게든 버티려고 합니다. 그러다 보면, 외부 전기장과 dipole에 의한 depolarizated electric field가 중첩이 생기는 상황이 발생하고 유전체 내의 Net electric field가 비약적으로 증가합니다. 다시 말해 강유전체가 가질 수 있는 전기장보다 훨씬 큰 전기장이 발생하게 됩니다. 이러한 상황이 잘 보이기 위해서는 polarization이 변화하는 시간이 유도되는 charge 변화하는 시간보다 빨라야 합니다. 문맥적으로 뭔가 모순되는 것처럼 보이지만, 위 그림에서 다룬 것은 net electric field에 대한 내용이고, 수식에서 다룬 내용은 Q입니다. 즉 Q 느리게 변화며 Q가 높게 유도된다라고 생각하면 이해가 될 겁니다. 가만히 생각해 보시면 단번에 이해될 것이라 믿습니다.
따라서 이런 효과를 확실하게 보기 위해서는 dQ/dt를 작게, 즉 Q를 천천히 변화게 해야 하는데, 이는 RC deley를 이용해서 제어할 수 있습니다. 강유전체 외부에 저항이나 커패시터를 직렬로 연결해 주면 됩니다. 따라서 Negative capacitance를 측정하기 위해서는 다음과 같은 회로로 구성하여 측정하면 됩니다.

다음과 같은 강유전체에 저항(Rs)을 연결해 준 회로에 위의 그림과 같은 전기장 pulse를 가해준 뒤, 강유전체 부분에 인가되는 저항만 오실로스코프로 측정을 합니다. 직렬로 연결된 저항은 Q의 변화를 지연시켜 주어 그냥 유전체의 경우에도 전압이 천천히 올라가게 만들어줍니다. 즉 R이 클수록 처음에 R에 흐르는 전류가 많아지어 R이 입력 Voltage의 대부분을 차지하게 됩니다. 그러다 점차 Capacitor에 전류 들어가며 Q가 쌓여 Q=CV만큼 Q가 쌓인다면, 입력된 pulse의 voltage를 함유할 수 있습니다. 하지만, 만약 Negative capacitance가 존재한다면, 강유전체에 인가되는 voltage가 커지는 과정에 polarization이 switching이 되지 않은 구간이 있어, 초반에 net electric field가 증가합니다. 그러다 polarization이 switching이 되고, 다시 유전체와 비슷한 양상을 띠며 증가하게 됩니다.
current를 측정하면, voltage의 미분과 비슷하게 나옵니다. 이 current를 다시 적분하면 Q를 구할 수 있는데, Q를 구한다면 다음과 같은 형태의 loop를 얻을 수 있고 끝 부분에서도 negative capacitance를 유추할 수 있습니다.
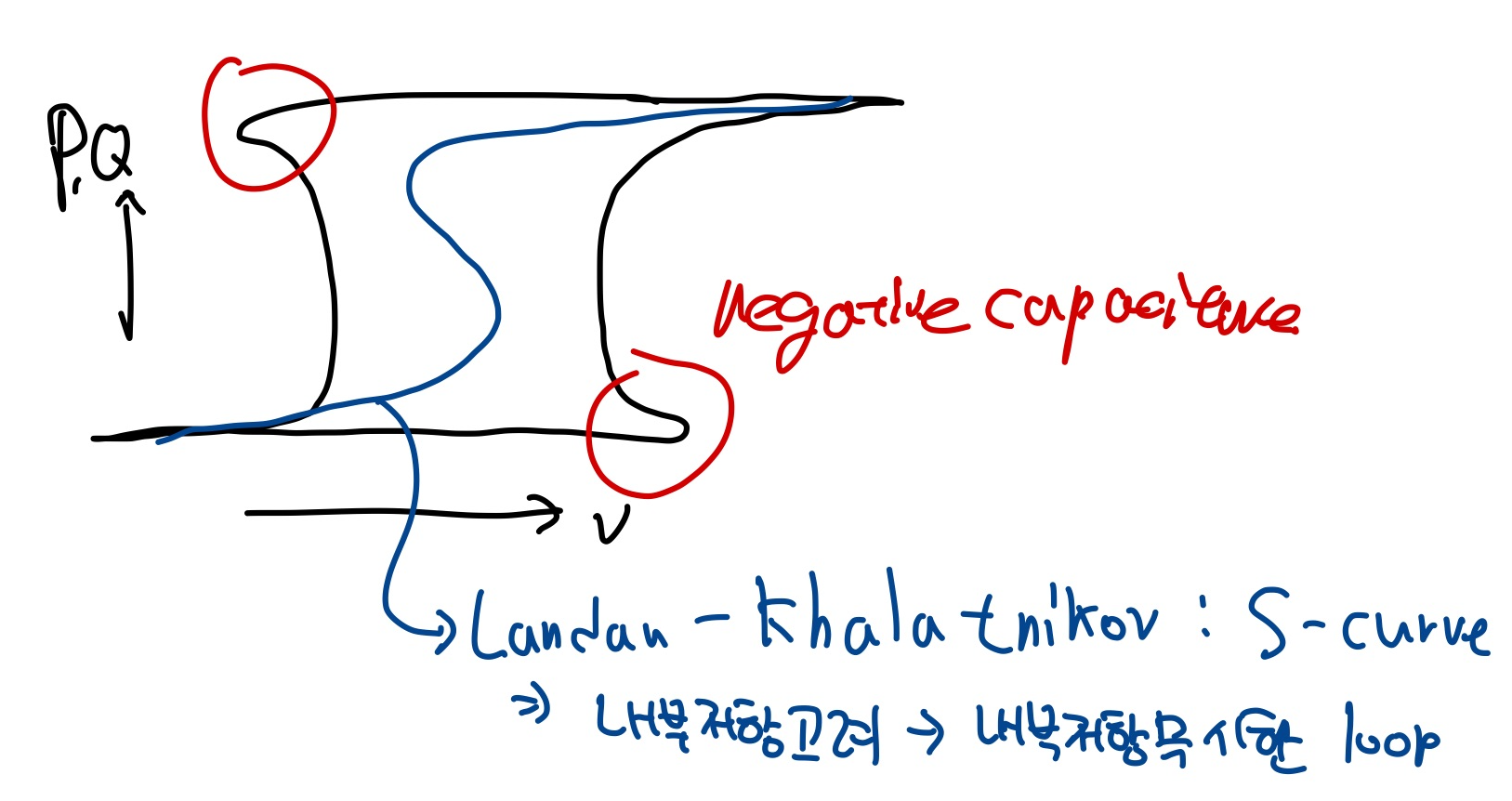
그냥 voltage로 Q를 구하면 안 되냐 생각하실 수도 있지만, 강유전체의 C가 계속 변화하기 때문에 전류를 따로 측정해서 적 분한 것이 정확합니다. 이때 완벽한 강유전체 물질이 없다는 것을 고려한다면 강유전체 내부에는 항상 내부 저항이 있는데, 이를 고려하여 polarization에 대한 경향만 추측할 수 있습니다. 이게 유명한 Landau-Khalatnikov(LK) 모델입니다.
갑자기 LK을 설명하여 엄청 뜬금없을 수가 있는데, 그래프의 이해를 위해 , 위 그래프에서 검은색을 측정을 한 것이고, 파란색이 fitting 한 것입니다. 파란색은 내부저항을 무시하여 피팅한 것인데, 이 피팅경향에서 negative capacitance를 유추할 수 있습니다. 다시 모델 설명으로 돌아가서 내부 저항이 있다면, 강유전체 물질에 걸리는 전압 Vf는
$$V_F=\frac{Q_F}{C_F(Q_F)}+\rho \frac{dQ_F}{dt},~\rho\frac{dQ_F}{dt}=-\frac{dU}{dQ_F}$$
여기서 강유전체에 대한 사항으로 기호마다 F를 붙였습니다. rho는 내부 저항에 대한 항입니다. 만약 저항이 없다면
$$\frac{dU}{dP_s}=0$$이 될 것이고 이 식을 전개해 본다면
$$2\alpha P_s+4\beta {P_{s}}^3=E_f\rightarrow \frac{dE_f}{dP_s}={(\varepsilon_f\varepsilon_0)}^{-1}=2\alpha +12\beta {P_s}^2$$으로 epsilon이 음수가 되는 negative capacitance의 영역을 유추할 수 있습니다. 이 외에도 polarization의 domain nucleation까지 고려하여 speed에 대한 고찰을 할 수 있는 Kolmogorov-Avrami-Ishibashi(KAI) 모델로 측정 데이터에 Fitting이 더 잘되는 이론이 있지만, 엄청나게 high-quality epitaxial film을 가정하고 논의가 복잡해질 수 있어 본 포스팅에서는 생략하겠습니다.
이제 인가하는 pulse의 speed에 대한 영향을 고려해 보겠습니다. Speed 볼 때는 작은 요소도 크게 영향을 미칠 수 있어 생길 수 있는 모든 요소를 고려해야 합니다. LK 모델에서 무시했던 내부저항을 다시 고려하고, 강유전체가 형성될 때 인접한 부분에서 자연산화가 되며 어쩔 수 없이 생기는 유전체를 고려해야합니다.

즉 DE+FE형태의 구조를 고려하여 다시 LK 모델을 가지고 옵니다. 당연히 내부저항을 무시하지 않고 이번에는 강유전체에 일반 유전체까지 형성된다고 가정을 하고 아까의 식을 전개해 본다면
$$\rho \frac{dP_s}{dt}=E_f-2(\alpha t_f+\frac{t_d}{2\varepsilon _d\varepsilon_0}P_s+4t_f\beta P_s^3$$
'물리학' 카테고리의 다른 글
| 강유전체 측정 ( Ferroelectric measurement ) (2) | 2020.01.17 |
|---|---|
| Polariton (0) | 2019.06.09 |
| Ferroelectricity (강유전체) (2) | 2019.05.27 |
| 초전도체 (superconductivity)_BCS model, Cooper pair, Josephson tunneling (0) | 2019.05.20 |
| Energy Band(에너지 밴드)_Tight Binding Model (1) | 2019.05.20 |



