| 가정 | Ferroelectricity (강유전체) |
| 요약 | |
| 응용 |
↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
요즘 엄청나게 급 부상하고 있는 강유전체(Ferroelectric) 물질을 어떻게 측정하는지 살펴보겠습니다.
익히 알려진 강유전체 물질이 아닌, 박막 형태, 유기물 형태의 강유전체를 측정하는 방법으로 준비물은
Function Generator와 Osciloscope만 있으면 됩니다.
Qiu et al. J. Appl. Phys. 113, 224106 (2013)이라는 논문의 그래프와 식을 차용하자면

박막 강유전체 물질은 Polarization되어있는 것 뿐 아니라, 각종 Defect에 의한 Conducting한 부분과, 온전히 Capacitor인 부분이 있을 것입니다. 전기적으로 본다면, 이들은 모두 전류에 기여할 수 있기 때문에, 이 강유전체 Sample에 전압을 가할때 흐르는 전류는
$$i_{sample}=i_{cap}+i_{p}+i_{cond}=C_s \frac{dV_s}{dt}+A_s\frac{dP_s}{dt}+\frac{V_s}{R_s}$$
로 나타낼 수 있습니다. 여기서 C는 sample의 Capacitance이고, V는 가한 Voltage, A는 Sample의 면적, P는 Polarization, R은 저항입니다.
이를 전하량 Q로 나타내나면 다음과 같습니다.
$$Q_{sample}(t)=Q_{cap}(t)+Q_p (t)+Q_{cond}(t)=C_sV_s(t)+A_sP_s(t)+\frac{1}{R_s}\int^t_0 V_s(t')dt'$$
위에서 구한 전류가 전하량을 구하는 방법은 두가지가 있습니다.

Method 1과 같이 Sample에서 나오는 전류를 직접 측정하는 방법과 Method 2와 같이 Sample에 커패시터를 직렬로 연결하여 커패시터 직렬연결에서 Q값이 같다는 것을 착안하여 즉정하는 방법이 있습니다.
보통 Method 1과 같은 방법은 Radiant사에서 제공하는 좋은 측정 장비로 문제없이 측정할 수 있습니다.
간단하게 Voltage to Current Convertor로 OP-AMP에 Feedback부로 저항을 달아 전류를 읽는 방법입니다.
Method 1은 단순히 전류를 읽는 것이고, 측정장비 자체의 회로적인 노하우가 많이 들어가므로 Method 2에 대해 보겠습니다.
사실 위 회로에서 커패시터 C1과 저항 Rm은 측정장비를 보호하는 역할로 측정에 관한 부분은 단순히 Cm만 보면 됩니다. 즉 간단하게 다음 회로를 가정하겠습니다.

그렇다면 전체 회로에 인가되는 전압은 샘플과 Cm에 걸리는 전압으로 분배될것 입니다.
$$V_{in} (t) = V_{out}(T)+V_{s}(t)$$
이때 Cm에 Sample보다 엄청나게 큰 Capacitance를 가진 커패시터를 연결한다고 가정을 한다면
$$C_{m}>>C_{1}\rightarrow V_s >> V_{m} \rightarrow V_{in}\approx V_{s}$$
입니다.
이떄 앞서 본 전하량은 두가지로 표현이 가능한데,
$$Q_{sample}(t)=C_sV_{in}(t)+A_sP_s(t)+\frac{1}{R_s}\int^t_0 V_{in}(t')dt'$$
$$Q_{sample}(t)=Q_{m}(t)=V_{m}(t)C_{m}=V_{out}(t)C_{m}$$
으로 이 두 전하량을 연립한다면,
$$V_{out}(t)C_{m}\approx C_{sample}V_{in}(t)+A_sP_s(t)+\frac{1}{R_s}\int^t_0 V_{in}(t')dt'$$
으로 Vout도 알고 Cm도 아는경우 Sample의 Cs와 Rs를 구한다면 Polarization Ps를 구할 수 있습니다.
이제 측정이 끝났고 측정데이터로 Cs와 Rs를 제거해 줄 수 있습니다. 이는 PUND라는 방법을 사용해야하는데, 입력 전압 신호를 다음과 같은 형태로 주어야 합니다,

이렇게 하는 이유는 단순히 Polarization을 분극 시킬 때 반대 분극으로 보낸뒤 분극이 Switching되는 상황을 만들기 위해서 그럽니다.
다시말하지면 다음데이터가 측정되었다고 가정할때,(다시 말씀드리지만 본 포스팅은 모두 Qiu et al. J. Appl. Phys. 113, 224106 (2013)의 데이터를 차용하였습니다.)
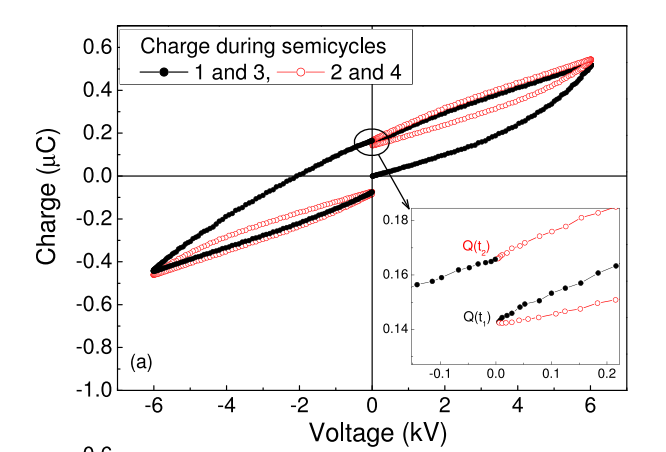
위와 같이 측정된것은 다시말해 위 PUND 신호에서 두번째 파부터 1, 2, 3, 4라 이름을 붙였을 때의 개형입니다. 사실이는 분극이 전혀 안되어있을때 부터 시작한 것인데, 1로 완전히 분극을 시킨뒤 다시 0으로왔다가 다시 완전히 분극이 된뒤 돌아온다면 이동안 앞서 보았던
$$\frac{1}{R_s}\int^t_0 V_{in}(t')dt'$$
가 쌓이게 됩니다. 따라서 위의 그래프에서 Q(t1)과 Q(t2)가 변화하게 되는데, 이 차이를 빼주는 저항을 빼주어야 합니다.
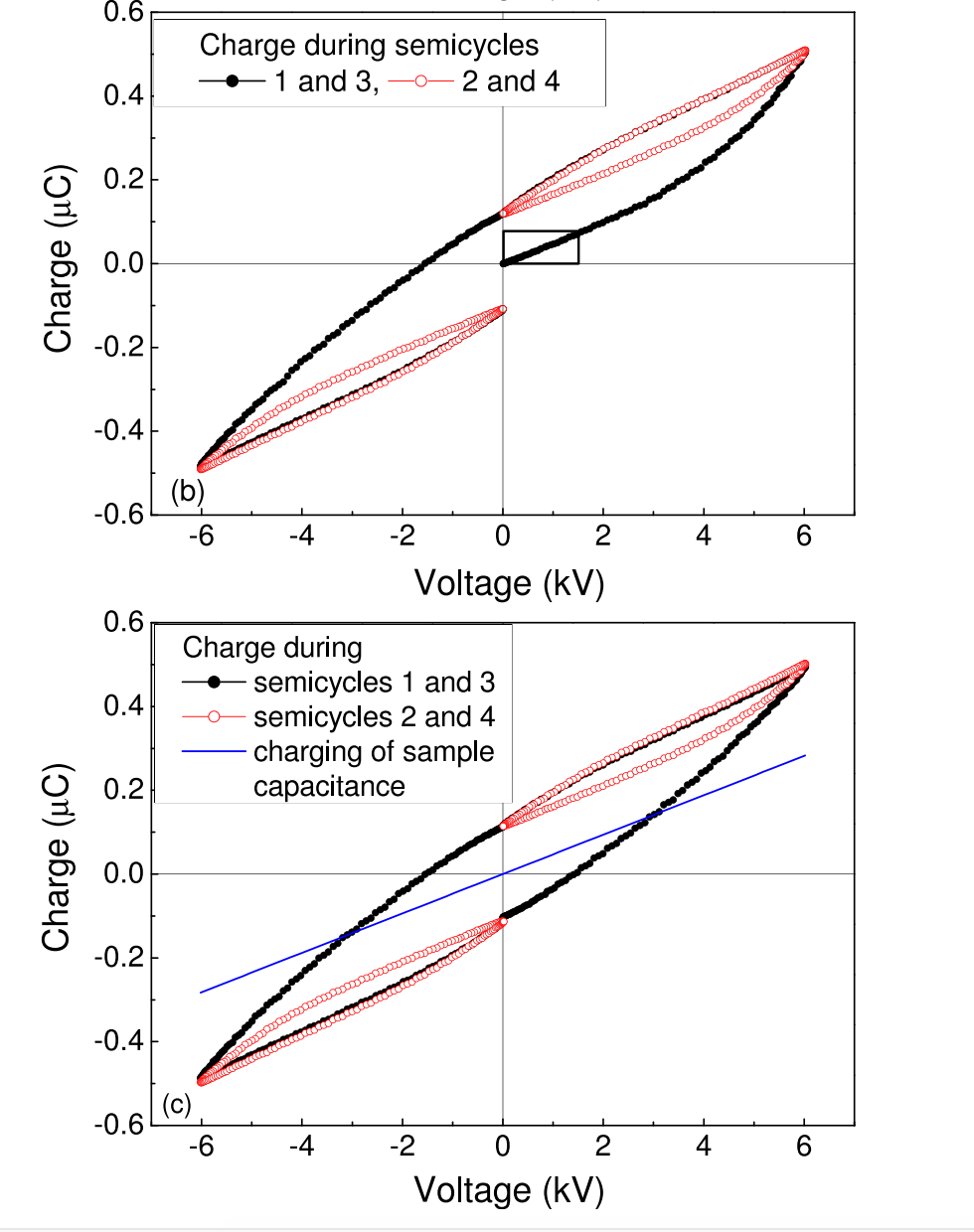
또한 다음 그래프에서 분극이 되지않고 처음 변화하는 네모 박스안에 Linear한 부분은 Sample자체의 Capacitance라 볼 수 있으므로 이를 빼주면 됩니다(파란색 직선 그래프)
만약 PUND로 측정되어있다면 이 Capacitance가 Voltage가 0인 부근에서 어느정도 같기 때문에 0인 부분의 기울기를 빼주면 됩니다.
'물리학' 카테고리의 다른 글
| 음의 전기용량 (negative capacitance) (8) | 2021.05.17 |
|---|---|
| Polariton (0) | 2019.06.09 |
| Ferroelectricity (강유전체) (2) | 2019.05.27 |
| 초전도체 (superconductivity)_BCS model, Cooper pair, Josephson tunneling (0) | 2019.05.20 |
| Energy Band(에너지 밴드)_Tight Binding Model (1) | 2019.05.20 |



