↑파란 박스의 글자를 클릭하시면 가정과 응용으로 넘어 가실 수 있습니다!!
Spintronics의 경우 아무래도 Spin을 다루어 소자를 제작하는 분야이므로 전기적인 측정이 많을 수밖에 없습니다.
사실 전기적인 측정은 특정한 공식과 메커니즘 속에 전압이나 전류가 있으면 이를 측정하여 확인하는 방법일 뿐 입니다.
다시 말해 공식으로 그린 그래프와 측정한 그래프가 맞으면 됩니다.
이 때 공식을 실제 메커니즘과 연결시키기 힘들수있는데, spintronics에 대해선 본 포스팅을 참조하시면 됩니다.
Spin을 가장 쉽게 측정하는 방법으로 SQUID(Superconducting Quantum Interference Device), VSM이나 MOKE (Mangeto-Optical Kerr Effect microscope) 와 같은 전자기 유도적 광학적으로 측정하는 방법이 있고 Second Harmonics나 ferromagnetic resonance (FMR)_magnetic resonance과 같이 전기적으로 측정하는 방법이 있습니다.
본 포스팅에서는 이 분석법을 실체 Spintronics 측정에서는 어떻게 이용되는지 다뤄보겠습니다. (여기서 NM=Nonmagnet, FM =Ferromagnet입니다.)
Spin 즉 magnet 물질에 대한 가장 기본적인 측정은 앞서 말씀드린 VSM과 SQUID(Superconducting Quantum Interference Device)입니다.
자성층 내부의 spin 이 얼마나 자성을 가지고 있고 어떤 방향을 선호하는지 알 수 있는 방법인데, 측정원리에 대해서는 본 포스팅에선 자세히 다루지 않겠습니다. 궁금하신 분들은 위 파란박스의 링크를 따라사기면 됩니다.(MOKE (Mangeto-Optical Kerr Effect microscope))
여기서 직접적으로 그려지는 그래프는 자기 이력곡선 (Hysteresis loop) _ 히스테리시스 곡선입니다. 앞 포스팅에서 다루었지만, 실제 특정하는 경우에서는 자성층 박막이 한개만 존재하지 않습니다. 예를들어 MTJ와 같은경우 여러 자성층이 겹쳐 아래와 같은 곡선이 나오기도 합니다.(두 그래프는 Nakano et al. Appl. Phys. Lett. 110, 012401 (2017)와 Jyotirmoy Chatterjee et al., SCIENTIFIC REPORtS (2018) 8:11724에서 참조하였습니다.)
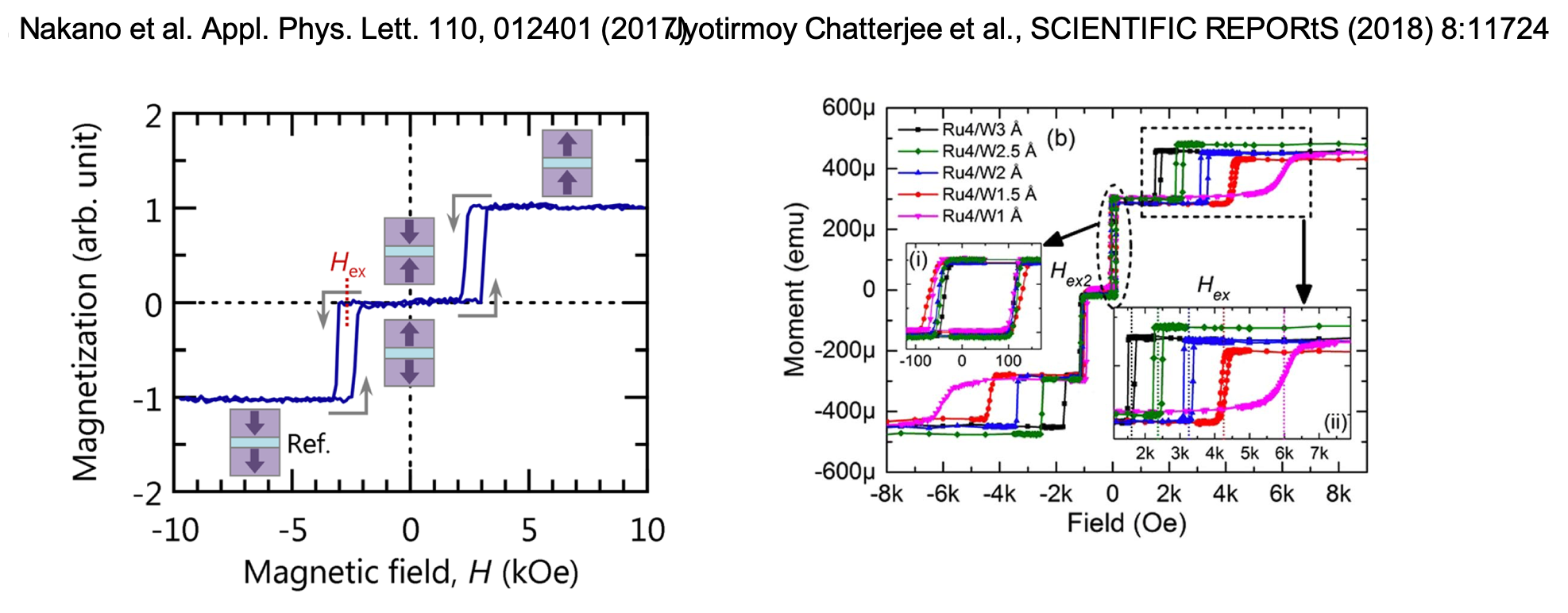
여러 자성층의 자기이력곡선은 단순히 Superpostion된다고 보면 됩니다. 다시말해 각각의 자기이력곡선을 단순히 더한다 생각하시면 됩니다. 여기서 이제 Antiferromagnet이나, SAF를 이용해 Exchange Bias를 가해 한 자성층의 곡선을 Shift를 시키는 등의 방법으로 제어할 수 있습니다.
중요한 것은 이 자성의 특성을 어떻게 표현하느냐 인데, 단순히 자기 이력곡선 (Hysteresis loop) _ 히스테리시스 곡선으로만 나타내지 않습니다. 자성에 관한 몇 논문을 보시면 간단하게 보실 수 있겠지만, 다음과 같은 자성특성에 관해선 아래 그림과 같은 그래프를 많이 보실 수 있을 겁니다.(그래프는 W Skowronski et al의 App. Phys. Express 8. 053003 2015를 가져왔습니다.)

Annealing Temperature 빼곤 모두 x축이 자성층 CoFeB의 두깨입니다. (CoFeB은 스핀트로닉스 물질 및 재료 (Spintronics material)에서 자세하게 다루니 궁금하신분은 들어가 보시기 바랍니다.)
왼쪽에서 부터 Keff t (mJ/m2), uMs (T), K(mJ/m2), M*t (mA/m*m) 을 y축으로 가지고 있습니다. 두께에 따라 자성값은 얼마나 감소하는지, 수직이방성에 대한 경향은 어떻게 변화하는지 볼 수 있습니다.
단순히 VSM 데이터인 자기 이력곡선에서 모두 뽑아낼 수 있는 데이터입니다만 경향성을 한눈에 볼 수 있습니다.
왼쪽 위의 그래프는 자기이방성 에너지를 나타낸 그래프로 y축의 값이 양수이면, Out of Plane이 easy axis이며, 음수이면, Inplane이 easy axis입니다. y축의 값의 크기는 자기 이방성 에너지로 얼마나 외부 자기장에 대해 잘 버티느냐를 알 수 있습니다.
자세한 내용은 자기 이방성 에너지(magnetocrystalline anisotropy energy)을 참조해주세요.
간략하게 언급하자면, VSM데이터에서 Saturation Magnetization [emu/cc]를 구하고, Hard axis에서 Hk값을 구한 뒤 K값으로 Ms와 Hk값을 곱하면 됩니다.
다음으로 Spin 거동을 전기적으로 확인할 수 있는 방법부터 다뤄 보겠습니다.
가장 쉽고 간단한 방법은 Anomalous Hall Measurement와 2nd Harmonics방법이 있는데,
Anomalous Hall Measurement는

NM(Normal metal)에서 Spin Hall Effect으로 일어나는 현상을 이용해 자성층의 Polarization을 전기적으로 알아보는 겁니다. (자세한 메커니즘은 스핀 홀 효과(spin hall effect, SHE)_Anomalous Hall effect(AHE), ISHE을 참고 부탁드립니다.)
십자가 형태를 가진 소자인데 이를 Hall bar라 합니다. 십자가 중 한 막대에는 전류를 흘리고, 다른 막대에서는 전압을 측정합니다.
NM의 전자들이 Spin up으로 polarization 되어있는 FM(Ferromagnet)으로 들어가며 FM내부에서 Spin filtering을 받아 spin up의 전자의 갯수가 우세해져 양단으로 이동하는 전자의 갯수가 차이나 전위차가 발생하는 것을 측정합니다.
이를 이용하면 Ferromanget 의 spin이 z방향인지 -z방향인지 알수 있습니다.
이때 전자의 양은 전류가 증가하며 점점 더 커지므로 Hall Voltage로 측정하는 것이 아닌, 인가한 전류로 나눈, Hall Resistance로 나타내는 것이 FM의 Polarization 특성을 나타냅니다. 이 경우 기존에 알고 있는 Normal Hall도 단순한 Slope로 나타나는데, 이는 단순히 그냥 기울기를 빼주면 됩니다. 반면, 측정을 하는 시간에 비례해 계속 저항이 높아진다면, 이는 열적인 효과이므로, 일정한 시간을 기다린후 측정을 해야합니다.
2nd Harmonics를 본다면, 이와 관련된 엄청나게 유명한 논문이 있습니다. 바로 2010년에 삼성에서 쓴 논문인데, Ung Hwan Pi의 Applied Physics Letters 97, 162507 (2010)입니다.
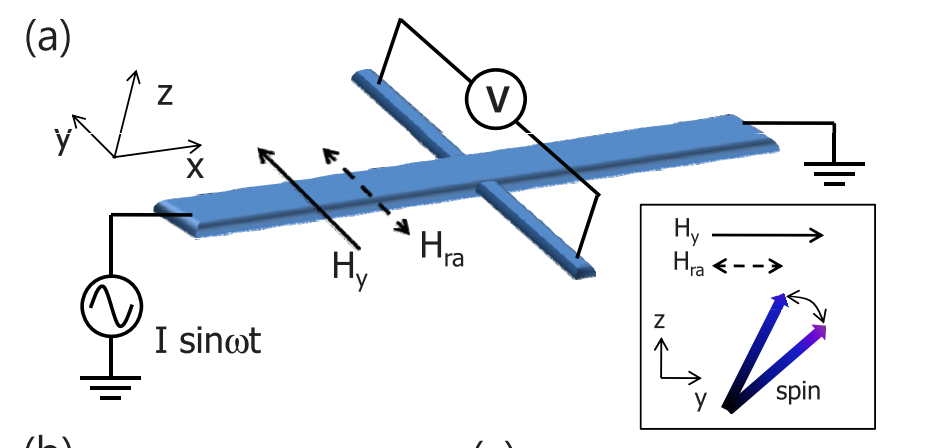
이 측정은 Hra 즉 Rashba Field를 측정하는 것인데, 더 넓게 본다면 Ferromagnet에 가해지는 Torque(Effective Field)를 보기위한 목적입니다.
NM/FM구조에서 전류가 흐르면 Rashba Field(Hra)가 생긴다고 가정하고, 전류가 동반됨에 따라 발생하는 전자기 유도의 Oesterd field는 Hra보다 작다는 것을 믿고 진행하기로 하겠습니다.
먼저 Hra에 대해 정확히 알아야 할 필요가 있습니다. 논문에 따르면, s-d coupling 세기에 따른 parameter를 P라 하고 Rashba interaction의 Coefficeint를 alpha_r이라 한다면, 전류밀도가 J일때
$$H_{ra} \approx \frac{\alpha _r P}{\mu_b M}(\hat z \times J)$$
라 할 수 있습니다. 즉 전류에만 이 Hra가 변동이 있다는 것을 알 수 있고 AC 전류를 준다면 이 나타나는 모든 Effective Field에서 Hra만 변화가 있을 것입니다.
Effective Field에 의한 FM내부의 Spin의 변동은 위에서 다른 Anomalous Hall Measurement에서 알 수 있으므로 Hall bar를 제작하여 Hall을 측정한다면, 어떻게든 Signal이 나타날 수 있음을 예상할 수 있습니다.
즉 위와같은 Hall Bar 구조에서 Hra와 같은 방향으로 외부 자기장 Hy를 가해준다면 이 외부자기장 Hy는 전류에 의해 변동되지 않습니다.
따라서 Anomalous Hall 저항이 Effective Field와 외부 자기장에 의해 Ferromagnet의 polarization이 tilting되어 변한다고 할때 이 저항은 자기장 H의 함수로 나타낼수 있습니다. R(H)
따라서 전류를 I sin wt를 준다고 할때 이 저항의 식은
$$R(H) = R(H_y + H_{ra}sin \omega t) \approx R(H_y)+\frac{dR}{dH}H_{ra}sin \omega t$$
입니다. 즉 저항은 주파수를 띄며 다음과 같이 변화합니다. 그러나 원래 Hall 측정에서는 전류를 가할때 저항이 일정합니다. 그런데 홀 저항이 저렇게 변화한다는것은 변화하는 항을 홀 저항과 별개로 검출할수 있다는 것입니다.
따라서 측정하는 주체인 Voltage는 어떻게 측정되는지 보겠습니다.
$$V(H)=R(H)\,I\, sin\omega t \approx [R(H_y)+\frac{dR}{dH}H_{ra}\,sin\omega t]\,I\, sin\omega t$$
$$=I\,\frac{dR}{dH}\frac{H_{ra}}{2}+C_\omega sin \,\omega t -C_{2\omega}cos\,2\omega t$$
입니다. 여기서 상수 C들은 다음과 같이 나타낼 수 있습니다.
$$C_\omega =IR,\,\,\,\,\,\,\,C_{2\omega}=-\frac{I\,H_{ra}}{2}\frac{dR}{dH}$$
로 Second Harmonics부분을 검출을 한다면 이차항의 C를 얻을 수 있고 Rashba에 의한 effective field를 구할 수 있습니다.
$$H_{ra}=-2\frac{C_{2\omega}}{dC_{\omega}/dH}$$
이 논문에서 결론이 많이 나와 있지만 가장 대표적이 경향을 볼 수 있는건 Baek S, Amin V, Oh Y et al., Nature Materials (2018) 17(6) 509-513의 논문결과 입니다.(사실 일본과 유럽이 더 잘설명되어있지만, 가장 최근 논문을 가져왔습니다.)
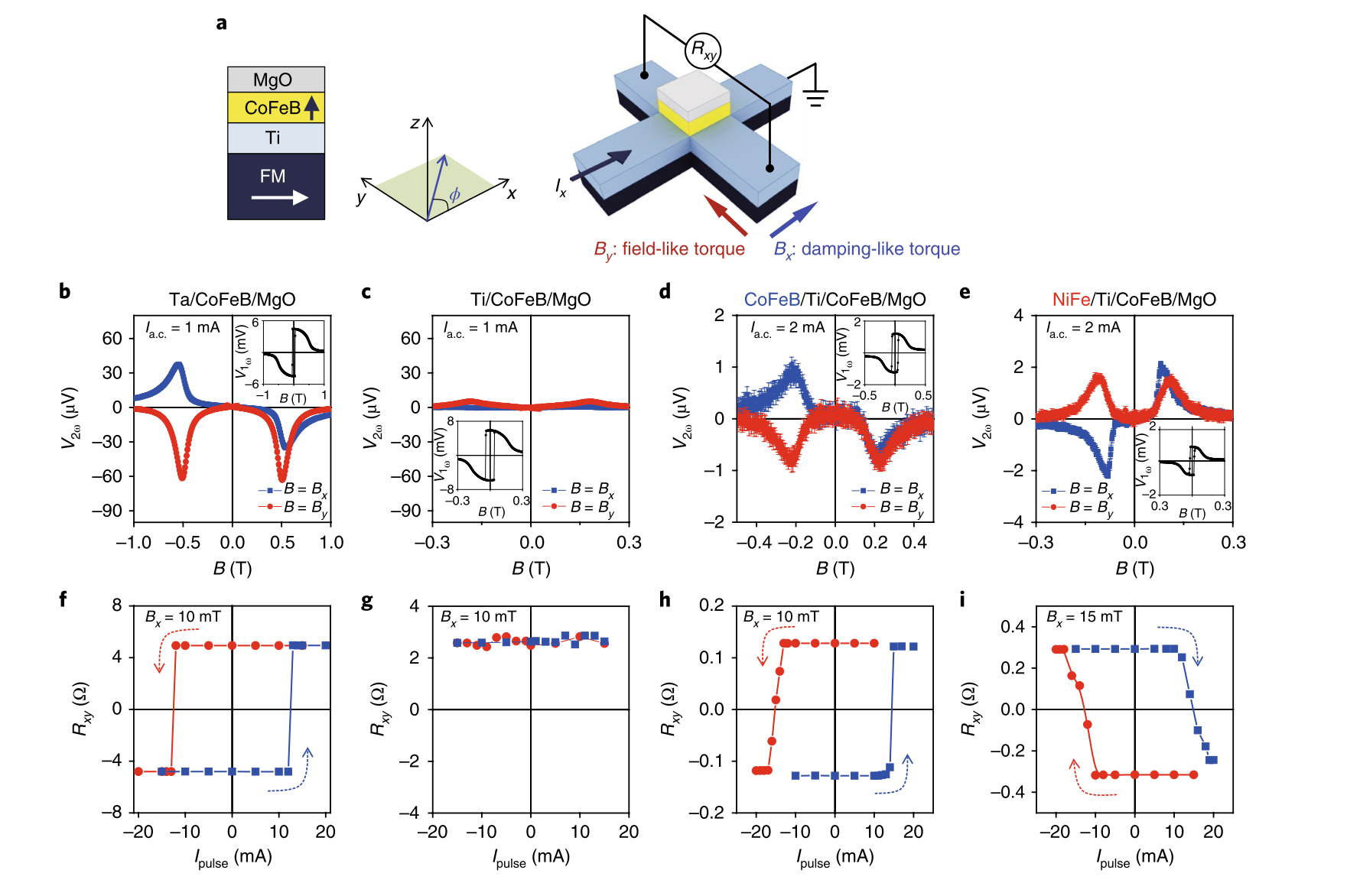
바로 이 결과 입니다. 간단하게 NM이 Spin current source로 쓴다는 것이 아닌 FM/Ti에서 (Ti는 직접 Spin current를 만들어 내지 않아 사용) FM/NM 계면에서 수직 Spin current가 생길 수 있다는 보인 논문입니다.
다시말해 FM/Ti에서 Spin current가 생겼다면 위 CoFeB에 Torque가 작용할 것이므로 다시말해 Effective Field가 생길 것이니 그것을 2nd Harmonics로 측정한 것입니다. (논문에 목적은 SOT-MRAM에 자세히 나와있습니다.)
참고로 위 그림b 안에 조그마하게 그려져 있는 것은 2nd Harmonics를 찍으며 동시에 측정한 1st Harmonics인 Hall 저항입니다. 저렇게 보이는 이유는 외부 Field가 phi만큼 각이져있어서 Switching을 하고 서서히 inplane으로 돌아눕기 때문입니다.(뒤에 나올 GST 측정 법이 이 그래프와 연결되어있습니다.)
참고로 phi는 이 논문에서는 Azimuthal angle라 합니다. 다시 본론으로 돌아가서 2nd Harmonics data만 본다면, 여기서는 저항이 아닌 Hall Voltage를 표기했습니다.
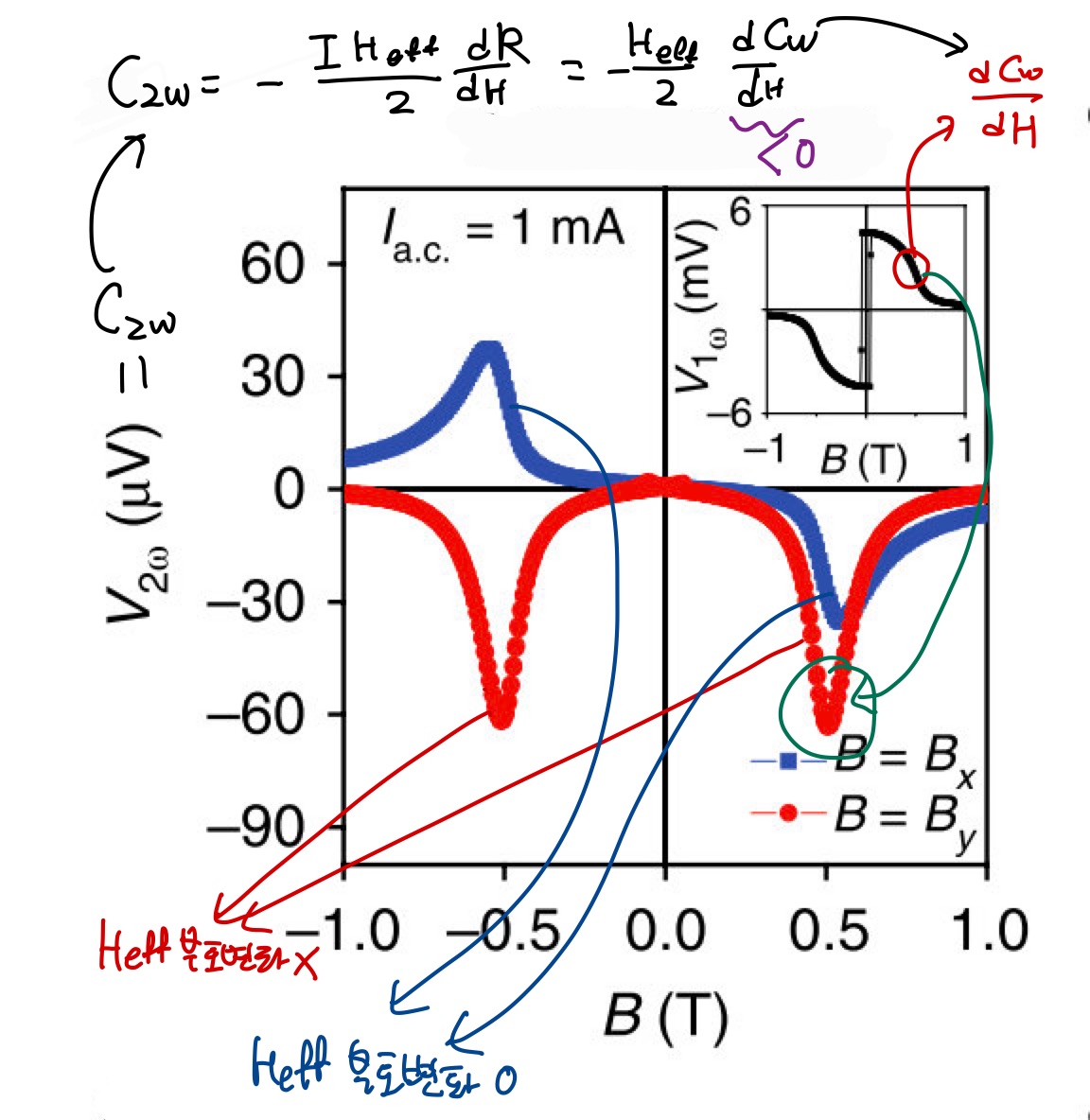
Hall Voltage로 표현한것은 부호의 변화 경향을 잘 확인할 수 있습니다. Peak부근은 단순히 Ferromagnet의 polarization이 Inplane으로 누울때 생기는 굴곡의 정도입니다.
하지만 여기서 외부 자기장이 양수(+)인지 음수(-)인지에 따라 외부 자기장에 방향에 대해 부호 경향이 다릅니다.
다시말해 Effective Field의 방향이 반대로 나온다는 것인데, 이 부호의 의미를 이해하기 위해서는 planer Hall Effect를 고려해야합니다.
2013년에 Gambardella 그룹에서 이에대해 nature nanotechnology 지에 자세히 연구내용을 서술한 논문이 있습니다.(Nature Nanotechnology volume 8, pages587–593(2013)) 이 논문을 기반으로 설명하겠습니다. 이 논문의 가장 대표적인 그림은 아래와 같습니다.

위 그림과 같이 hall bar에서 한쪽 bar에 전류를 가해주고 다른쪽 bar에서 전압을 측정한다면, 다음과 같은 식을 만족해야합니다.
$$V_H = R_{AHE}Icos(\theta)+R_{PHE}Isin^2\theta sin 2 \phi$$
여기서 AHE은 anormalous hall effect이고 PHE는 Planar hall effect 입니다.(planar Hall effect (PHE, 플레이너 홀 효과) _ pseudo hall effect참조)
위에 했던 방법으로 이차항을 끄집어낸다면
$$R^{2f}_H=(R_{AHE}-2R_{PHE}cos\theta sin 2\phi )\frac{d cos\theta}{d B_{ext}}\frac{B_\theta}{sin (\theta_B-\theta)}+2R_{PHE}sin^2\theta cos2\phi \frac{B_\phi}{B_{ext}sin_{\theta_B}}$$
여기서 각도를 돌리거나 계산으로 PHE를 유추할 수 있다면,PHE을 0으로 보내고 1차 AHE 수식을
$$R_{AHE}\frac{d \, cos\theta}{dB_{ext}}=\frac{dR_H^f}{dB_{ext}}$$
로 고칠 수 있으므로 $$B_{\theta}$$를 2nd harmonics식에서 유추할 수 있습니다.
논문에서는 $$\theta_B$$를 82도로 설정하였는데, 가장 이상적인 상황은 90도 이나, 90도로 설정시 magnetic domain이 생길수 있어 이렇게 설정해 두었습니다.
$$\phi$$를 바꾸면서 측정을 한다면, 측정 결과가 field like torque인지, damping like torque인지 구분해 낼 수가 있습니다. 만약 0도이면(전류와 외부 자기장 방향이 같다면), damping like torque가 더 많은 영향을 표현하고, 90도 이면 field like torque가 더 많은 영향을 줍니다. 이는 torque와 effective field관계를 잘 계산해보면 알수 있으며, 직관적으로 자화 반전 (magnetic switching) : field free switching을 참조하면 이해가 됩니다.(사실 m이 흔들리는 정도에 대한 AHE 차이를 보는 방법이므로 외부 자기장을 한쪽으로만 고정시켜 놓는다면 effective field는 그 방향에서만 m을 움직이게 될겁니다. )
위 그림의 파란색과 빨간색으로 이루어져있는 그래프를 보시면, 맨 왼쪽은 모든 torque이 섞여있는 그래프이고 중간 그래프(빨강)는 field like toqure를, 맨 오른쪽(파랑)은 dampling like torque을 나타냅니다. 0도에서는 dampling like toque만 나오는게 확인이 되며, 90도 에서는 field like torque만 나옵니다. 경향자체만 놓고 본다면 (모두 계산된 결과 이지만)
$$b^{\perp}\approx -cos\theta \, sin\phi, \,\,\,\,\, B^{||}\approx cos\phi$$
입니다.
다음으로 수직 자기 이방성 에너지를 측정할 수 있는 방법인 GST에 대해 다루어 보겠습니다.
ST FMR
Oscilator측정
Domain wall velocity
BLS
가속기
Switching detect(TMR)
XRMS
BLS in Spintronics
'Review' 카테고리의 다른 글
| SOT-MRAM (0) | 2020.08.01 |
|---|---|
| 뉴로모픽 컴퓨팅 (Neuromorphic Computing) _ 인공지능 (0) | 2020.07.27 |
| [특집] 전류 (0) | 2019.09.10 |
| [특집] Ferromagnetic vs Ferrimagnetic vs Antiferromagnetic Spintronics (0) | 2019.06.13 |
| 자성학 (스핀트로닉스) 공식 정리 (0) | 2018.08.20 |


